Объяснение:
S(бок)= S(МDА)+S(МDС)+S(МАВ)+S(МСВ)
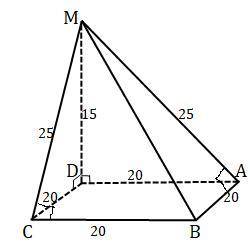
1)Т.к. МD⊥(АВС) , то МD⊥DА , МD⊥DС.
Δ МDА= МDС как прямоугольные по 2-м катетам : МD-общая, АD=DС как стороны квадрата , S(МDА)=S(МDС)=1/2*20*15=150(см²).
2) МD⊥( АВС), DА⊥АВ , значит МА⊥АВ по т. о 3-х перпендикулярах⇒ΔМАВ-прямоугольный.
МD⊥( АВС), DС⊥СВ , значит МС⊥СВ по т. о 3-х перпендикулярах⇒ΔМСВ-прямоугольный.
3) ΔМАВ= ΔМСВ, как прямоугольные по катетам МА=МС=25 и общей гипотенузе МВ. Поэтому S(МАВ)=S(МСВ)=1/2*20*25=250 (см²).
4)S(бок)= 2*150+2*250=800 (см²).
Диагонали квадрата равны и точкой пересечения делятся пополам:
ОА = ОВ.
Если проекции наклонных, проведенных из одной точки, равны, то равны и сами наклонные.
ОА - проекция МА на плоскость квадрата, ОВ - проекция МВ, значит
МА = МВ, т.е. ΔМАВ равнобедренный.
Пусть Н - середина АВ. Так как треугольник МАВ равнобедренный, то МН - его медиана и высота.
ОН = 0,5AD = 9 см как средняя линия ΔDAB.
ΔМОН: ∠МОН = 90°, по теореме Пифагора
МН = √(МО² + ОН²) = √(144 + 81) = √225 = 15 см
Smab = AB · MH / 2 = 18 · 15 / 2 = 135 см²