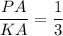 ⇒ KA = 3PA
⇒ KA = 3PA
По свойству пересекающихся хорд :
PA * KA = NA * MA
PA * 3PA = 16 * 3
PA² = 16 ⇒ PA = 4 см
KA = 3PA = 3*4 = 12 см
PK = PA + KA = 4+12 = 16 см
Самая большая хорда в любой окружности - это диаметр. Поэтому диаметр не может быть меньше любой из хорд, проведенных в окружности.
В данной окружности проведено 2 хорды :
MN = MA + NA = 3 + 16 = 19 см
PK = 16 см
Значит, наименьшее значение диаметра не может быть меньше 19 см.
Тогда наименьший радиус равен 19 : 2 = 9,5 см
ответ: РК = 16 см; наименьший радиус 9,5 см
Первая часть выше решена, по поводу решения второй части (наименьшее значение радиуса)
PK = 16 см
MN = 19 см - это наибольшая хорда
если центр окружности (пусть будет точка O) соединить с точками M и N, а OM = ON = r (радиус окружности)
Тогда по теореме косинусов MN^2 = r^2 + r^2 - 2r^2Cosα, где Cosα - угол между OM и ON.
2r^2(1 - Cosα) = 19^2, наименьший радиус будет в том случае, если (1 - Cosα) - наибольшее (-1 <= Cosα <= 1), т.е. Cosα = -1 (α = 180 - когда MN - диаметр)
Получим r = 19/2 = 9.5 см