, найденный нами катет является меньшим, поэтому вращение треугольника происходит вокруг него, при этом образуется конус. Осевое сечение конуса представляет собой равнобедренный треугольник, в котором боковые стороны равны образующей, а основание равно диаметру окружности, лежащей в основании конуса, в данном случае образующая равна гипотенузе, диаметр-двум большим катетам данного треугольника, а высота-меньшему катету, значит площадь сечения равна: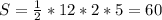
5х=150
х=150/5
х=30
∠К=30°, ∠L = 60°, ∠M=90° ⇒ KL - большая сторона.
2. ∠DEC=180-120 = 60°
sin∠DEC= DC/ DE
√3/2 = 5/DE
DE=5/(√3/2) = 10/√3
3. Вопрос: как указана точка N? Отрезки будут равны, если являются радиусами окружности с центром в т. N, а стороны треугольника являются касательными к этой окружности (перпендикуляра проведены в точки касания). В другом случае, эти перпендикуляры отсекают подобные треугольники (по двум углам), но не равные.