Объяснение:
Вспомним теорему о сумме углов, прилежащих к боковой стороне трапеции:
Углы, прилежащие только к боковой стороне трапеции, в сумме составляют 180°.
В этой задаче у нас фигурируют части. Складываем части:
3 + 2 = 5 частей - всего.
Теперь давайте найдем, сколько градусов приходится на каждую часть.
Для этого 180° разделим на 5 частей.
180° : 5 = 36° - приходится на каждую часть.
Теперь 36° умножаем на 2 и 3.
36° * 2 = 72° - меньший угол трапеции;
36° * 3 = 108° - больший угол трапеции.
Задача решена.
Объяснение:
Вспомним теорему о сумме углов, прилежащих к боковой стороне трапеции:
Углы, прилежащие только к боковой стороне трапеции, в сумме составляют 180°.
В этой задаче у нас фигурируют части. Складываем части:
3 + 2 = 5 частей - всего.
Теперь давайте найдем, сколько градусов приходится на каждую часть.
Для этого 180° разделим на 5 частей.
180° : 5 = 36° - приходится на каждую часть.
Теперь 36° умножаем на 2 и 3.
36° * 2 = 72° - меньший угол трапеции;
36° * 3 = 108° - больший угол трапеции.
Задача решена.
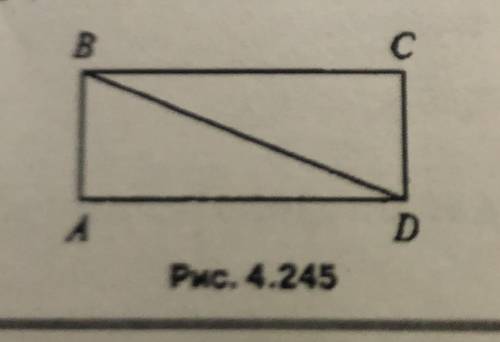
четырехугольнике АВСD ∠ВАD=∠BCD=90°
∠ADС=∠ADB+∠CDB=90°
Сумма углов четырехугольника 360°.=>
∠АВС=360°-3•90°=90°
Четырехугольник АВСD - прямоугольник. Противоположные стороны прямоугольника параллельны. => АВ║СD
или:
∆ АВD прямоугольный, угол АDB=15°,⇒ ∠ABD=90°-15°=75°
Углы, образованные прямыми АВ и СD и секущей BD, – накрестлежащие и равны.
По признаку параллельности прямых АВ║CD, ч.т.д.