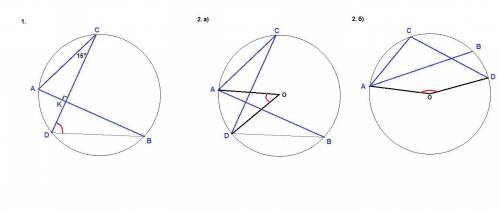
1. ∠BDC = 75°
2. а) ∠AOD = 30°
б) ∠AOD = 170°
Объяснение:
1. Пусть К - точка пересечения хорд.
ΔАКС: ∠АКС = 90°, ∠АСК = 15°, ⇒
∠САК = 90° - 15° = 75°
∠САВ = 75° - вписанный,
∠BDC = ∠CAB = 75° как вписанный, опирающийся на одну дугу с углом САВ.
2. а) ∠AOD = 2∠ACD = 2 · 15° = 30°, так как вписанный угол равен половине центрального, опирающегося на ту же дугу.
б) ∪AD = 2∠ACD = 2 · 95° = 190°
∪ACD = 360° - ∪AD = 360° - 190° = 170°
∠AOD = ∪ACD = 170°, так как центральный угол равен дуге, на которую опирается.
Площадь правильного треугольника находится по формуле
где a - длина стороны треугольника
Площадь любой из граней пирамиды равна
или
1)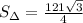
Площадь боковой поверхности равна сумме трех площадей правильного треугольника со стороной 11 см.
3)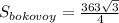
4) Площадь полной поверхности равна сумме четырех площадей правильного треугольника со стороной 11 см.
или
2) Объем найти сложнее. Нужна высота пирамиды.
Высоту можно найти из прямоугольного треугольника, образованного высотой пирамиды (это катет), Стороной (боковой гранью) пирамиды (гипотенуза) и частью высоты треугольника, лежащего в основании пирамиды (второй катет). Такой треугольник будет прямоугольным, так как высота перпендикулярна всей плоскости основания пирамиды (в том числе и отрезку, соединеящему основание высоты и боковую грань-как раз второй катет.). Нам нужно найти второй катет. Высота пирамиды падает на центр и вписанной и описанной окружности. Так как пирамида правильная. Это будет пересечение биссектрис или серединных перпендикуляров. В правильном треугольнике точка пересечения биссектрис совпадает с точкой пересечения медиан. А медианы в точке пересечения делятся в отношении 2 к 1 считая от вершины. Значит длина второго катета равна 2/3 высоты правильного треугольника со стороной 11 см. Высота правильного треугольника равна по формуле
В данном случае
2/3 от этой высоты равна
По теореме Пифагора найдем первый катет в прямоугольном треугольнике
Объем пирамиды находим по известной формуле