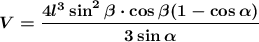
Объяснение:
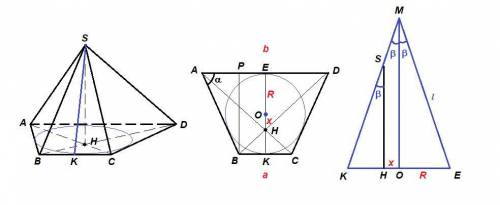
Центр окружности, вписанной в равнобедренную трапецию, лежит на середине отрезка КЕ (точки К и Е - середины оснований).
Так как точка пересечения диагоналей лежит на том же отрезке, но ближе к меньшему основанию, высота пирамиды лежит на образующей конуса, проходящей через точку К.
Высота трапеции равна диаметру вписанной окружности, а суммы противолежащих сторон равны.
Итак, ВР = КЕ = 2R,
AB + CD = AD + BC
AD = b, BC = a.
Чтобы найти высоту пирамиды, надо знать длину КН, а для этого найти расстояние между центром окружности и основанием высоты пирамиды ОН = х.
ΔАВР: ∠АРВ = 90°,
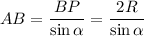
AP = BP · ctg α = 2R · ctg α
Тогда
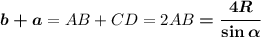
Так как по свойству равнобедренной трапеции
АР = (AD - BC) / 2, то
b - a = 2AP = 4R · ctg α
ΔAHD ~ ΔCHB по двум углам, тогда их высоты относятся как сходственные стороны:
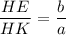
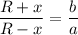
a(R + x) = b(R - x)
aR + ax = bR - bx
x(a + b) = R(b - a)
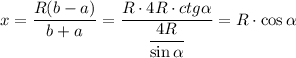
KH = R - x = R(1 - cos α)
Справа на рисунке осевое сечение конуса, проходящее через хорду КЕ.
∠KSH = ∠KMO = β как соответственные при SH║MO и секущей КМ.
SH = KH · ctg β = R(1 - cos α) · ctgβ
Итак, объем пирамиды:
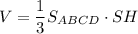
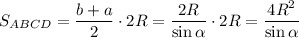
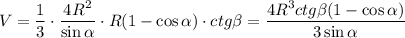
Осталось из прямоугольного треугольника МОЕ выразить R:
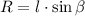
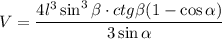
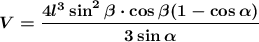
Объяснение:
4.
Дано: ABCDA₁B₁C₁D₁ - правильная призма.
А₁С =4 - диагонали призмы;
∠DA₁C=30°
Найти: Sбок.
1. AD ⊥ DC (основание - квадрат)
Теорема о трех перпендикулярах: прямая, проведенная в плоскости через основание наклонной перпендикулярно к ее проекции на эту плоскость, перпендикулярна и к самой наклонной.⇒ A₁D ⊥ DC
2. Рассмотрим ΔA₁CD - прямоугольный.
Катет, лежащий против угла в 30°, равен половине гипотенузы.⇒ DC = A₁C : 2 = 2
По теореме Пифагора:
3. Рассмотрим ΔАА₁D - прямоугольный.
По теореме Пифагора:
Площадь боковой поверхности найдем по формуле:
Sбок.=Росн.·h, где Р - периметр основания, h - высота призмы.
Sбок. = 8 * 2√2 = 16√2 (ед.²)
5.
Дано: ABCDA₁B₁C₁D₁ - правильная призма.
А₁С - диагонали призмы;
∠DA₁C=30°; DC = √2
Найти: V призмы.
1. Рассмотрим ΔA₁CD - прямоугольный. (см. задачу 4)
Катет, лежащий против угла в 30°, равен половине гипотенузы.⇒ А₁С = √2 · 2=2√2
По теореме Пифагора:
Найдем V пирамиды: