РЕШЕНИЕ
сделаем построение по условию
AB = BC , так как ABCD -квадрат
Точка M делит сторону BC в отношении 1:2 -можно считать ,
что сторона ВС состоит из 3-х равных частей.
Точка E делит сторону AB в отношении 1:3 - можно считать ,
что сторона АВ состоит из 4-х равных частей.
Прямая CE пересекает стороны AM и MD треугольника AMD в точках К и L соответственно.
Дополнительное построение :
обозначим точку М1 - середина отрезка MC , тогда BM=MM1=M1C
проведем через точки М, М1 прямые m, m1 параллельные прямой CE
по теореме Фалеса :
параллельные прямые m,m1,CE отсекают на сторонах угла <EBC
пропорциональные отрезки
на стороне ВС : BM=MM1=M1C , значит на стороне BE тоже три равные части
обозначим для так как сторона АВ состоит из 4-х равных частей, то любая часть может быть
представлена в виде 3х , тогда BE=3x, тогда ЕА=9х, тогда отношение 1 : 3 = 3х : 9х = 3 : 9
рассмотрим угол <BAM
снова теорема Фалеса, снова параллельные прямые m,m1,CE , снова
пропорциональные отрезки на сторонах угла
MK : KA = 2x : 9x = 2 : 9 <это сторона АМ треугольника AMD
Дополнительное построение :
проведем прямую DM до пересечения с прямой АВ - точка Р
проведем прямую DN параллельную прямой CE
прямая DN отсекает на прямой АВ отрезок AN
CE || DN , EN || CD
NECD - параллелограмм , так как противоположные стороны попарно параллельны
следовательно BE=AN , тогда BE : EN = 1 : 4
т. е. отрезок BN состоит из 5-и равных частей.
тогда BE=3x, тогда ЕN=12х, тогда отношение 1 : 4 = 3х : 12х = 3 : 12
рассмотрим угол <NPD
снова теорема Фалеса, снова параллельные прямые m,m1,CE,DN , снова
пропорциональные отрезки на сторонах угла
ML : LD = 2x : 12x = 2 : 12 = 1 : 6 <это сторона МD треугольника AMD
ОТВЕТ
для стороны АМ отношение 2 : 9
для стороны МD отношение 1 : 6
Подробнее - на -
Объяснение:
Пирамида правильная. Значит, основанием данной пирамиды является правильный многоугольник, а вершина проецируется в центр этого многоугольника.
Апофемой называется высота боковой грани, проведенная из вершины правильного многогранника.
Центр правильного треугольника - точка пересечения его высот, являющихся в правильном треугольнике медианами и биссектрисами.
а)
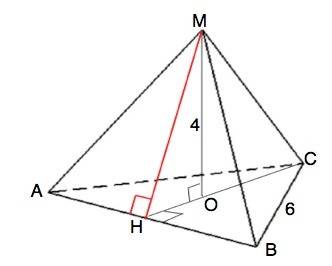
На рисунке в приложении О - центр основания. СН - высота ( медиана). Медианы треугольника точкой пересечения делятся в отношении 2:1, считая от вершины.
Следовательно, отрезок СО=2/3 высоты СН, отрезок ОН=1/3 высоты СН.
Все углы правильного треугольника равны :180°:3=60°
CН=СВ•sin60°=6•√3/2
CO=6√3/6=√3
ОН перпендикулярна АВ и является проекцией МН на плоскость АВС. По теореме о трёх перпендикулярах МН⊥АВ. =>
МН высота ∆ АМВ, т.е. апофема данной правильной пирамиды.
Высота пирамиды перпендикулярна основанию. => МО⊥СН.
Из прямоугольного ∆МОН по т.Пифагора
МН=√(МО²+НО²)=√(16+3)=√19 (ед. длины)
б)
Все боковые грани правильной пирамиды - равные равнобедренные треугольники. => их площади равны.
S (AMB)=MH•AB:2=√19•6:2=3•√19
S(бок)=3•3√19=9√19 (ед. площади)
Большая часть морей находится в западной части океана вдоль Евразии: Берингово, Охотское, Японское, Жёлтое, Восточно-Китайское, Филиппинское.