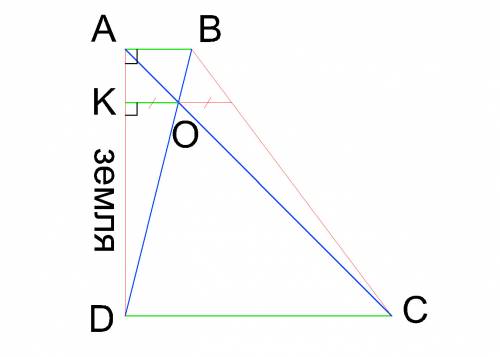
Шесты АВ и ДС как основания образуют прямоугольную трапецию АВСД, а пересечение канатов ВД и СА есть не что иное, как пересечение диагоналей прямоугольной трапеции.
Как известно, отрезок, параллельный основаниям и проходящий через пересечение диагоналей прямоугольной трапеции делится точкой пересечения пополам, и если АВ=х, ДС=у, то длина его равна 2·х·у/(х + у).
Исходя из этого: ОК=2·х·у/(х + у)÷2=х·у/(х + у)
1) ОК=(х·у)÷(х + у)
Как видно, длина ОК никаким образом не зависит от расстояний между шестами, а лишь от их высоты.
2) Если AB=х=2 м, а DC=у=8 м, то ОК=(2·8)÷(2+8)=1,6 м
ответ: длина шеста ОК=1,6 м
Треугольники АВК и CДМ равны т.к. АВ=СД, ВК=ДМ и ∠В=∠Д. В них ∠АВР=∠СДЕ, значит ВР=ДЕ.
Пусть одна часть в заданном отношении равна х, тогда ВР=ДЕ=2х, РД=3х, РЕ=РД-ДЕ=3х-2х=х.
В тр-ке ВСЕ РК║СЕ, ВР:РЕ=2:1, значит ВК:СК=2:1 - это ответ 1.
Параллельно сторонам АД и ВС через точку Р проведём отрезок НО.
Параллельно сторонам АВ и СД к прямой НО проведём отрезок КТ.
НВКТ - параллелограмм. Его площадь равна двум площадям треугольника BPК т.к. у них одинаковая высота к стороне ВК.
S(НBКТ)=2S(BРК)=2.
Площадь параллелограмма ТКСО равна половине НВКТ т.к. КС=ВК/2.
S(TKСО)=2/2=1.
АНОД - параллелограмм. Соответственно его площадь равна удвоенной площади тр-ка АРД.
Тр-ки BPК и АРД подобны по трём углам, значит их коэффициент подобия k=ВР:РД=2:3, а коэффициент подобия площадей k²=4/9.
S(АРД)=S(BРК)/k²=9/4.
S(АНОД)=2·9/4=4.5,
Площадь исходного параллелограмма АВСД равна сумме площадей найденных параллелограммов НВКТ, ТКСО и АНОД.
S(АВСД)=2+1+4.5=7.5 - это ответ 2.