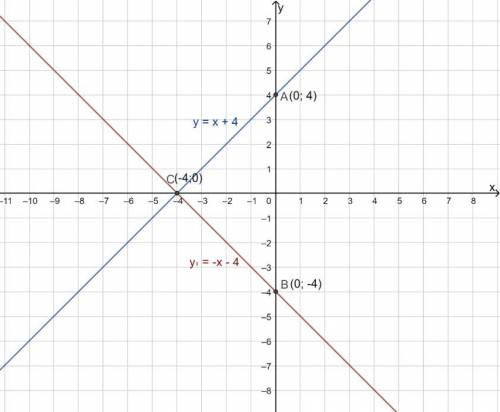
График линейной функции y₁ = -x - 4 будет симметричен графику линейной функции y = x + 4 относительно оси OX. Оба графика являются прямыми линиями.
Решение.
Функция y = x + 4 является линейной функцией, ее график прямая линия, область определения ее множество всех чисел D(y) = (-∞; ∞), коэффициент k = 1, k >0 график пройдет через I - III четверти.
Для построения прямой достаточно найти координаты двух точек графика: при x = 0, y = 4; при x = -4, y = 0.
По условию луч OX является осью симметрии. При осевой симметрии прямые переходят в прямые.
⇒ фигура, симметричная графику функции y = x + 4 также будет являться прямой, которая описывается формулой y₁ = -x - 4.
Точки A и B, симметричные относительно оси OX (лежат на одном перпендикуляре к оси OX на равных расстояниях от нее).
Точка A(0;4) перейдет в симметричную ей точку B(0;-4).
Точка С(-4;0) лежит на оси OX и отобразится сама на себя.
1) Рассмотрим ∆PQR. PQ=QR=> ∆PQR - равнобедренный.
Периметр ∆PQR=100=PQ+QR+PR
PR+26+26=100
PR=100-26-26=100-52=48
2. Из вершины Q ∆PQR проведем высоту QH, которая одновременно медиана и биссектриса,
т.к. ∆PQH=∆QHR(PH=HR, QR=PQ, QH- общая).
Значит, в ∆PQH по теореме Пифагора PQ²=PH²+QH²
26²=QH²+24²
QH²=26²-24²=(26+24)(26-24)=50×2=100
QH=√100=10
3. S∆PQR=(QH×PR)/2=(48×10)/2=48×5=240
ответ: 240.