. Найдите длину перпендикуляра, проведенного из точки S к гипотенузе AB, если SC=3.
Объяснение:
Каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к этому отрезку.
Расстояние от точки до прямой на плоскости — это кратчайшее расстояние от точки до прямой и равно длине отрезка, который соединяет точку с прямой и перпендикулярен прямой.
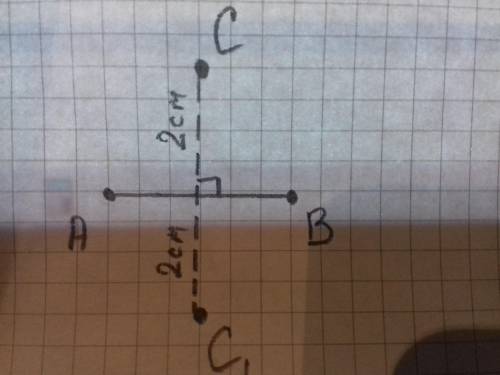
Отсюда можно сделать вывод, что ГМТ будут две симметричные точки, лежащие на серединном перпендикуляре на расстоянии 2см от АВ каждая.
В прикрепленном файле это точки С и С₁
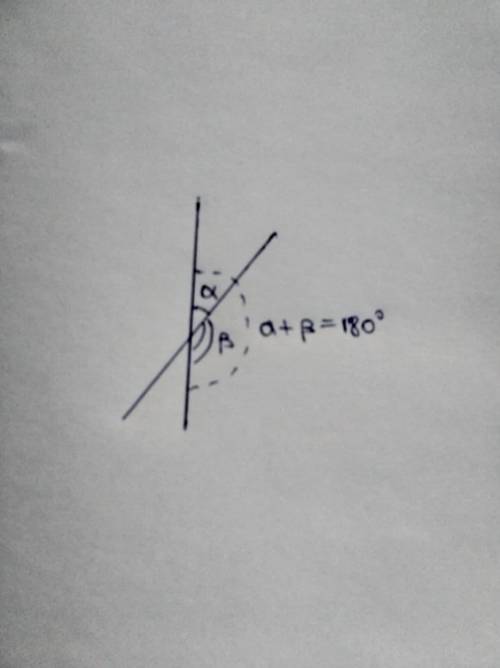
При пересечении двух прямых появляются вертикальные углы.
Одно из свойств вертикальных углов - противоположные углы при их создании равны
Рассмотрим пример: на фото ниже мы видим вертикальные углы на практике. При создании вертикальных углов пара малого и большего угла создают развёрнутый угол в 180°.
Как мы видим, при разности углов данной пары противоположные углы равны, отсюда - равенство лишь двух углов
Рассмотрим наши требования. Если провести перпендикуляр с какой-либо точки, увидим следующее: перпендикуляр создаёт угол в 90°. Соседний прямой угол прямого угла создают в сумме 180°. Продолжая перпендикуляр по идентичной траектории, увидим, что на обратной стороне прямой будут такие же прямые углы. Следуя по таким соображениям, мы можем заметить, что все углы равны и наши условия пересечения двух прямых полностью справедливы и действительны
Что и требовалось доказать
Длина перпендикуляра от т.S к гипотенузе равна 5
Объяснение:
AB=AC*√2=4√2*√2=8 гипотенуза.
СМ=АВ/2=8/2=4 высота и медиана ∆АСВ.
Медиана прямоугольного треугольника равна половине гипотенузы.
По теореме Пифагора
SM=√(SC²+MC²)=√(4²+3²)=√(16+9)=
=√25=5