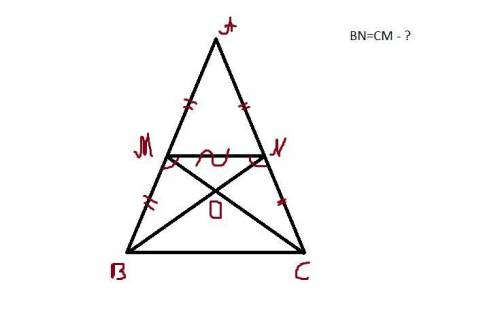
Т.к. АВ=АС , то треугольник равнобедренный
Прямая MN - средняя линия треугольника, значит она разбивает стороны АВ и АС на равные отрезки, которые также равны между собой
Прямая MN отделяет от треугольника АВС равнобокую трапецию BMNC с диагоналями BN и МС. А т.к. трапеция равнобокая, то ее диагонали равны, т.е. BN = МС, ч.т.д.
Или же можно продолжить доказывать равенство этих прямых через ПРТ (треугольники на рассмотрение: BMN и CNM). У них MN - общая сторона; BM=NC и ∠BMN = ∠CNM (как односторонние углы равнобокой трапеции). Отсюда ΔBMN = ΔCNM по 1 ПРТ, значит, BN = МС, ч.т.д.
Два треугольника равны по третьему признаку равенства треугольников, если ...
Выберите один из 3 вариантов ответа:
1) две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника ;
2) сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника ;
3) три стороны одного треугольника соответственно равны трём сторонам другого треугольника.
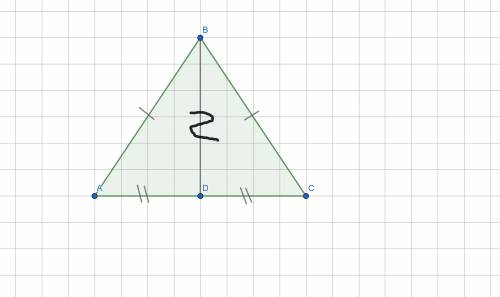
ответ: 3).Задание №2.Дано:ΔABD и ΔCBD;
AB = BC;
AD = DC.
Доказать:ΔABD = ΔCBD
Доказательство:1. AB = BC (по условию) |
2. AD = DC (по условию |⇒ ΔABD = ΔCBD (по третьему признаку).
3. BD - общая сторона |
Что и требовалось доказать!
ответ: 2).