1. Рассмотрим два случая: 1) прямые а и b пересекаются и лежат в плоскости β. Обе прямые параллельны плоскости α. Если плоскость проходит через прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения параллельна данной прямой. Проведем через прямую а плоскость (розовую), пересекающую плоскость α по прямой а'. Согласно выше приведенной теореме, а'║a. Проведем через прямую b плоскость (зеленую), пересекающую плоскость α по прямой b'. b'║b. Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то плоскости параллельны.
2) прямые а и b параллельны и лежат в плоскости β. Обе прямые параллельны плоскости α. Из этого не следует, что плоскость β параллельна плоскости α. На рисунке приведен пример, опровергающий утверждение, что плоскости в этом случае параллельны.
Утверждение: если две прямые, которые лежат в одной плоскости, параллельные второй плоскости, то эти плоскости параллельны - неверно.
2. Точки Е и К лежат в плоскости одной грани. Соединяем их. Точки Р и К так же соединяем. КЕ и КР - отрезки сечения. Найдем точку пересечения прямой КР с плоскостью АВС: КР лежит в плоскости грани SBC, эта плоскость пересекает плоскость АВС по прямой ВС, значит строим точку пересечения прямой ВС и прямой КР - это точка М. Точки М и Е, принадлежащие сечению, лежат в одной плоскости АВС, значит прямая МЕ - линия пересечения секущей плоскости с плоскостью АВС. ЕС пересекает ребро АС в точке F. Соединяем P и F, и E и F. KPFE - искомое сечение.
1. Правильный четырехугольник - квадрат.
Диаметр вписанной в квадрат окружности равен стороне квадрата. ⇒ r=d:2=4:2=2 см.
Для описанного вокруг данной окружности треугольника АВС она - вписанная.
Радиус вписанной в правильный треугольник окружности равен 1/3 его высоты. Следовательно, высота ∆ АВС =2•3=6 см.
Тогда АВ=ВН:sin60°=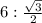
=4√3 см.
* * *
2. Для нахождения площади сектора существует формула.
S=Lr:2, где L – длина дуги сектора. ⇒
S=6•4:2=12 см²
Если формула забыта, решить задачу можно без нее.
Длина окружности C=2πr
C=2•p•4=8π см
Площадь окружности S=πr²=16 π см²
Вычислим площадь, которая приходится на сектор с дугой в 1 см.
S:C=16π:8π=2
Тогда площадь сектора
S=2•6=12 см²