A)Допустим, это не так. Тогда точки A₁0₁B₁0₂ лежат в одной плоскости. Тогда в ней же лежат прямые, проходящие через O₁;O₂ параллельные A₁B₁ или, что то же самое, параллельные CD В частности, там лежат середины ребер AD и DD₁ ни вместе с A₁ задают плоскость грани куба AA₁D₁D, в которой не лежит B₁. Противоречие.
б)Введем координаты с началом в точке A и с осями x,y,z, направленными вдоль прямых AD,AB,AA₁ соответственно. Тогда координаты точек будут такими: A₁(0,0,2),B₁(0,2,2),O₁(1,1,0),O₂(2,1,1). Если отложить вектор A₁B₁ от точки B₁, то его конец T будет иметь координаты (1,3,0). Написав уравнение плоскости, проходящей через B₁,O₂,T, получим x+y+z-4=0. Тогда расстояние от точки (0;0;2) до этой плоскости составит 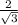
Объяснение:
1). в
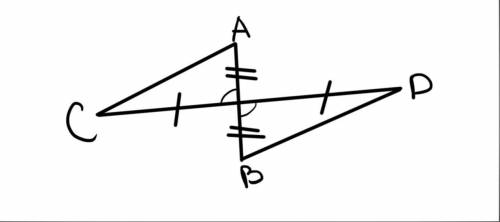
2). (рис 1) Доказываем равенство ΔCOA и ΔBOD по двум сторонам и углу между ними:
AO = OB (по условии)CO = OD (по условии)∠AOC = ∠BOD (как вертикальные углы)из этого ⇒ CA = BD = 4см
PΔCAO = CO + AO + CA = 5+3+4 = 12см
3). ABCD - параллелограмм. Поэтому ∠A=∠C по признаку параллелограмма(противолежащие углы равны)
4). тут я немного не понял. написано что ∠A и ∠C равны, потом пишут, что надо доказать что они равны...
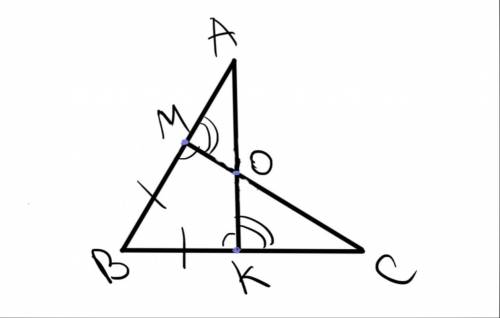
5). (рис 2) Доказываем равенство ΔABK и ΔCBM по стороне и двум прилежащих сторон:
BK = BM (по условии)∠B - общий∠BMC =∠BKA (по условии)из этого ⇒ AK = CM = 9, BC = AB = 15, CK = BC - BK = 15 - 8 = 7
AK = AO + OK = CM = MO + OC = 9 ⇒ MO = OK, AO = OC ⇒ OK + OC = 9
PΔCOK = OK + OC + CK = 9 + 7 = 16
132
Объяснение:
обозначим угол С как х
тогда В-х+18
тогда А-(х+18)*4
х+х+18+4х+72=180
6х=90°
х=15°