ответ:Решение.
а) Обозначим буквой E точку пересечения отрезков MK и AB. Углы ∠ALB и ∠LAD равны, как накрест лежащие углы; аналогично ∠CLD = ∠ADL, как накрест лежащие. Отсюда получаем, что ∠BAL = ∠BLA, ∠CDL = ∠CLD, то есть треугольники ABL и CLD равнобедренные (AB = BL, CL = CD). Тогда биссектрисы этих треугольников BM и CK являются также высотами и медианами. Значит, точки M и K являются серединами сторон AL и DL соответственно. Отсюда следует, что отрезок MK является средней линией треугольника ALD. Значит, MK || AD.
Теперь если рассмотреть треугольник ABL, получаем, что отрезок EM параллелен стороне BL и исходит из середины стороны AL. Отсюда следует, что EM является средней линией этого треугольника, а значит точка E — середина стороны AB. Что и требовалось доказать.
б) Рассмотрим 4-угольник MLKN. Из предыдущего пункта получили, что ∠M = 90°, ∠K = 90°, откуда следует, что
То есть у данного 4-угольника суммы противоположных углов дают , откуда следует, что вокруг него можно описать окружность. Соединим точки N и L (пересечение с MK в точке F) — получим 2 прямоугольных треугольника NML и NKL. Тогда центр описанной окружности лежит на середине общей гипотенузы NL.
Теперь заметим, что треугольники MFL и NFK подобны по 2 углам (∠MFL = ∠NFK, как вертикальные; ∠MLF = ∠NKF, как вписанные углы, опирающиеся на одну и ту же дугу MN). Тогда
Аналогично треугольники NMF и KFL подобны по 2 углам (∠NFM = ∠KFL, как вертикальные; ∠MNF = ∠FKL, как вписанные углы, опирающиеся на одну и ту же дугу ML). Тогда
Поделим соотношения друг на друга:
Из подобия треугольников NLC и NFK (по 3-м углам) получим, что Аналогично из подобия треугольников NLB и NFM получим, что , откуда следует:
Окончательно получаем, что
ответ: 5 : 14.
Объяснение:
Площадь полученного шестиугольника будет меньше площади данного шестиугольника на шесть площадей равных равнобедренных треугольников. У этих треугольников боковые стороны равны ½ стороны данного шестиугольника, а угол между ними равен 120⁰.
SΔ= ½ ab · sin γ
S = ½ · ¼a² · (√3)/2 =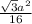
(кв.ед.)
Из формулы площади шестиугольника S=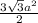
выражаем сторону а:
Подставляя в формулу площади треугольника, находим, что SΔ = 8/3 кв.ед.
6SΔ = 16 кв.ед.
Площадь полученного шестиугольника равна 64-16=48 (кв.ед.)