ответ: 5400см²
Объяснение:
Боковыми гранями правильной усеченной пирамиды являются равные равнобедренные трапеции. Для нахождения площади боковой поверхности нужно найти высоту этих трапеций.
Для нахождения боковой поверхности усечённой пирамиды надо:
S (усеч пирамиды) = S (трап. АА1С1С)*3
S (трап. АА1С1С) =(А1С1+АС)/2*НН1
В треугольнике АВС т.О - центр вписанной окружности и по свойству медиан делит ВН в отношении 2:1, считая от вершины
см фото

ответ: время=t=4часа; скорость=v=6км/ч
Объяснение: пусть первоначальная скорость туриста,=х, а время=у. Увеличенная скорость=х+2, а итоговое время =у-1. Зная, что в первом и во втором случае он пройдёт 24км, составиим уравнение:
Первоначально запланировано=ху;
С изменениями=(х+2)(у-1):
(х+2)(у-1)=ху
ху-х+2у-2=ху
ху-ху-х+2у=2
-х+2у=2
х-2у= -2
х=2у-2
Подставим значение х во вторую часть уравнения:
(2у-2)у=24
2у²-2у=24 |÷2
у²-у=12
у²-у-12=0
D=1-4(-12)=1+48=49
y1=(1-7)/2= -6/2= -3
y2=(1+7)/2=8/2=4.
Значение у1 нам не подходит поскольку время не может быть отрицательным, поэтому используем у2 =4. Мы нашли первоначальное время и теперь найдём первоначальную запланированную скорость туриста:
Так как v=s÷t, то:
v=24÷4=6км/ч
Проанализируем каждое утверждение.
1) Сумма смежных углов равна 180°. Если смежные углы равны, то каждый из этих углов равен по 180°:2 = 90°.
ответ: утверждение 1 верно.
2) Если диагонали какого-нибудь четырёхугольника точкой пересечения делятся пополам, то этот четырёхугольник - параллелограмм. Трапеция не является параллелограммом. Следовательно, это неверно.
ответ: утверждение 2 неверно.
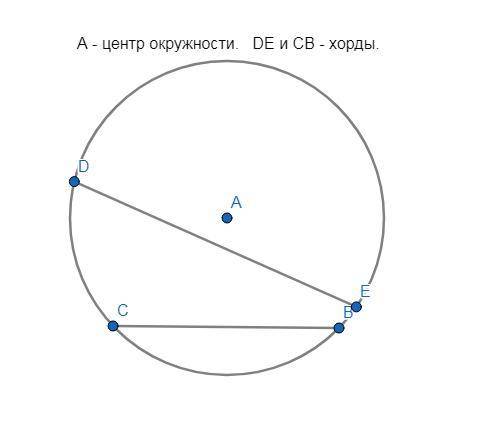
3) Хорда окружности - отрезок, соединяющий любые две точки, лежащих на окружности. Они могут располагаться на разных расстояниях от центра окружности, следовательно, также иметь разную длину.
ответ: утверждение 3 неверно.
ответ: 1.
Відповідь:
5400 см^2.
Пояснення:
Боковые грани правильной усеченной треугольной пирамиды - это трапеции с основаниями 60 см. и 120 см. Найдем высоту трапеции.
Рассмотрим вид сверху на пирамиду.
Треугольник АВС имеет угол В - прямой, угол С = 30° и сторону ВС = 30 см.
АВ = 30 × tg 30° = 17,32 см.
Если посмотреть на пирамиду сбоку, то высота пирамиды и отрезок АВ - это катеты треугольника, гипотенузой которого является высота трапеции ( боковой грани усеченной пирамиды ).
Н = sqrt ( 10^2 × 17,32^2 ) = sqrt 400 = 20 см.
Вычислим площадь боковой грани
Sтр = ( 60 + 120 ) / 2 × 20 = 1800 см^2.
Площадь боковой поверхности нашей пирамиды равна трем площадям трапеции.
S = 3 × Sтр = 3 × 1800 = 5400 см^2.