Для решения нужно найти сторону основания и апофему.
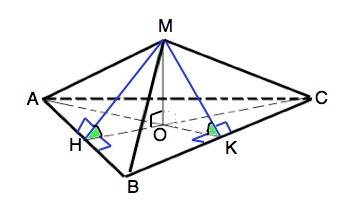
Основание правильной треугольной пирамиды МАВС - равносторонний треугольник АВС.
СН=5 ⇒
СВ=СН:sin60°=5:√3/2=10/√3
Вершина правильной пирамиды проецируется в центр основания,
т.е. в точку пересечения медиан ∆ АВС.
По свойству медиан т.О делит СН в отношении СО:ОН=2:1 =>
ОН=CH:3=5/3
Данный по условию двугранный угол - угол между боковой гранью и основанием, а ребром его является сторона основания.
Градусной мерой двугранного угла является величина линейного угла, стороны которого – лучи с общим началом на ребре двугранного угла, проведенные в его гранях перпендикулярно ребру.
Наклонная МН⊥АВ, её проекция СН⊥АВ, ⇒ угол МНО=45°
∆ МОН- прямоугольный.
cos45°=√2/2
Апофема МН=ОН:cos45°=(5/3):(√2/2)
S(ABC)=CH•AB:2=5•5/√3=25/√3
S(бок)=3•МН•АВ=3•10/(3√2)•0,5•10/√3=25√2/√3
S(полн)=S (осн)+S(бок)
S(полн)=25/√3+25√2/√3 =25•(1+√2):√3= ≈ 34,846 см²
Как всегда, надо построить треугольник, равновеликий трапеции. Это делается так - из вершины малого основания проводится прямая, параллельная диагонали, не проходящей через .то вершину, до пересечения с продолжением большого основания. Получатеся треугольник, у которого основание равно сумме оснований трапеции, а боковые стороны - суть диагонали трапеции. Ясно, что площадь этого треугольника равна площади трапеции (у них одинаковые средние линии и общая высота).
То есть нам надо найти площадь треугольника со сторонами 20, 15 и 7. (Это РАЗНОСТЬ двух Пифагоровых треугольников (9,12,15) и (12,16,20), площадт которых равны 54 и 96, разность 96 - 54 = 42)
Если тупо считать по Герону.
Полупериметр p = (20 + 15 + 7)/2 = 21; p - 20 = 1; p - 15 = 6; p - 7 = 14;
S^2 = 21*14*6*1 = 42^2; S = 42.
2,7мм
Объяснение:
42мм переводим у сантиметри = 4,2 см
АС=АВ-СВ
АС=4,2-1,5=2,7см