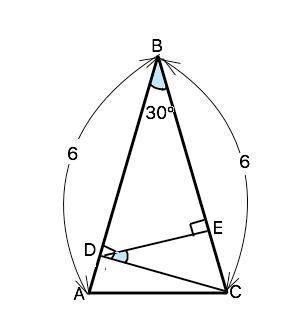
В равнобедренном треугольнике ABC угол В равен 30°, AB=BC=6, проведены высота CD треугольника ABC и высота DE треугольника BDC. Найдите BE.
——————————
ответ: 4,5 (ед. длины)
Объяснение:
Из ∆ ВDC катет DC противолежит углу 30° ⇒ DC=ВС:2= 6:2=3 (свойство).
Высота прямоугольного треугольник, проведенная к гипотенузе, делит его на треугольники, подобные друг другу и исходному треугольнику. Сумма острых углов прямоугольного треугольника 90°.
Угол BСD=90°-∠DBC=90°-30°=60°, угол ЕDC=30°.
CD - гипотенуза прямоугольного ∆ СЕD, катет ЕС противолежит углу 30°,⇒ ЕС=СD:2=3:2=1,5 ⇒
ВЕ=6-1.5=4,5
Или:
Катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и проекцией катета на неё.
СD²=BC•EC. Из найденного СD=3.
3²=6•CE ⇒ CE=1,5 a BE=BC-CE=6-1,5=4,5
ответ: 337,5 см²
Объяснение:
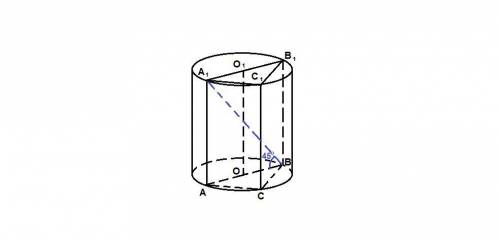
Так как цилиндр описан вокруг призмы, то основания призмы вписаны в основания цилиндра, боковое ребро призмы является высотой цилиндра.
Площадь полной поверхности цилиндра - это сумма площади боковой поверхности и площади двух оснований:
Sпов = 2πRh + 2 · πR²
Центр окружности, описанной около прямоугольного треугольника лежит на середине гипотенузы. Значит, радиус основания цилиндра равен половине гипотенузы:
ΔАВС: ∠С = 90°, по теореме Пифагора:
АВ = √(АС² + ВС²) = √(9² + 12²) = √(81 + 144) = √225 = 15 см
R = 1/2 AB = 7,5 см
Большая грань призмы - грань, содержащая гипотенузу основания.
Так как диагональ прямоугольника АВВ₁А₁ делит прямой угол пополам, то АВВ₁А₁ - квадрат. Тогда
h = AA₁ = AB = 15 см
Sпов = 2πRh + 2 · πR² = 2π · 7,5 · 15 + 2π · 7,5² =
= 225π + 112,5π = 337,5π см²
На какие отрезки разделяет точка E отрезок AB. ( У задачи есть два решения.)
решение №1: AF CE AE EF EB
решение №2: EA EC BE FE CE
Задание 3 Отрезок. Длина отрезка. Треугольник Математика 5 класс
На какие отрезки разделяет точка C отрезок AF. ( У задачи есть два решения.)
решение №1: EC CF AE AC EB
решение №2: EA BE CA FC CE
Задание 4 Отрезок. Длина отрезка. Треугольник Математика 5 класс
Найди длину отрезка AB, если известно, что AC равен 4 сантиметра, CD в два раза длинее чем AC, а DB на два сантиметра больше чем CD.
1) AB = см
Найди длину отрезка AB, если известно, что CD равен 12 сантиметра, AC в два раза короче чем CD, а DB на 3 сантиметра больше чем CD.
2) AB = см
Задание 5 Отрезок. Длина отрезка. Треугольник Математика 5 класс
Таблица перевода единиц измерения. откроется в новом окне.
Выразите в сантиметрах.
1) 3 дм 4 см= см 2) 14 дм 8 см = см 3) 4 м 3 дм 1 см = см 4) 14 м 7 дм 2 см = см Задание 6 Отрезок. Длина отрезка. Треугольник Математика 5 класс
Таблица перевода единиц измерения. откроется в новом окне.
Выразите в милиметрах.
1) 1 дм 2 см= мм 2) 23 дм 6 см 2 мм = мм 3) 1 м 1 см 3 мм = мм 4) 11 м 3 дм 5 мм = мм Голосование Отрезок. Длина отрезка. Треугольник Математика 5 класс