AC₁=2
AD₁=√5
Объяснение:
1. Рассмотрим ΔАВС (см. рис. 1). Он равнобедренный с АВ=ВС=1 и ∠В=120° (как внутренний угол правильного шестиугольника). Опустим высоту ВО на АС. Получили два равных прямоугольных ΔАВО = ΔСВО с углами 60°, 30° и 90° (т.к. ВО в равнобедренном тр-ке есть биссектрисой).
По теореме Пифагора,
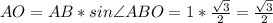
тогда АС=АО*2=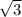
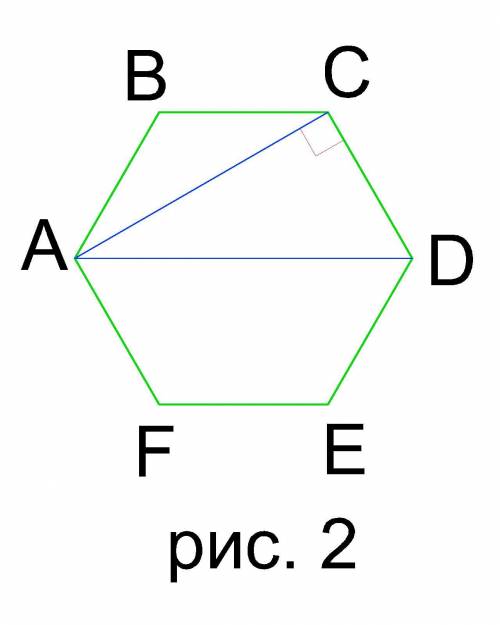
Рассмотрим ΔACC₁ (см. рис. 3). Он прямоугольный с двумя известными катетами
АС=√3, CC₁=1. Гипотенуза АС₁ является искомой величиной.
По теореме Пифагора: 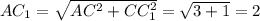
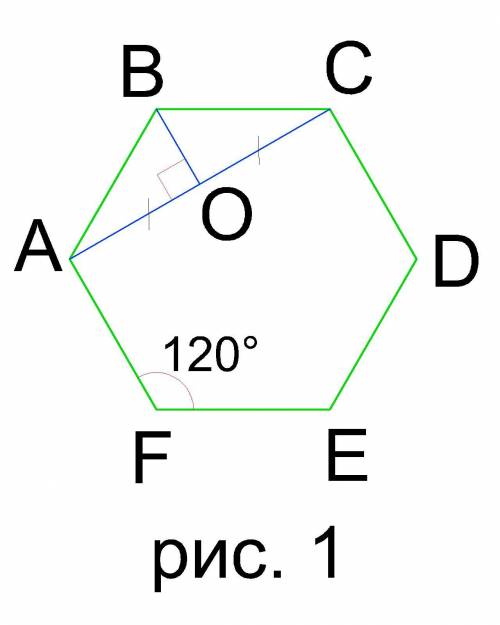
2. Рассмотрим ΔACD. Он прямоугольный с двумя известными катетами
АС=√3, CD=1 (см. рис. 2). Найдем гипотенузу АD.
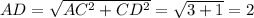
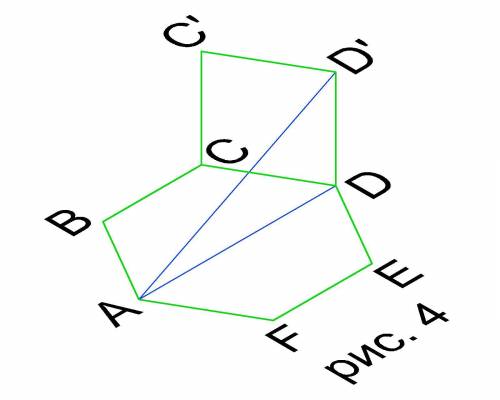
Рассмотрим ΔADD₁ (см. рис. 4). Он прямоугольный с двумя известными катетами
АD=2, DD₁=1. Гипотенуза АD₁ является искомой величиной.
По теореме Пифагора: 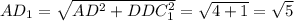
расстояние от точки С до точки касания вписанной окружности равно (a+b-c)/2 , у нас (b-c=1) известно
потом обозначить за x недостающее расстояние от вершины до точки касания и записать 2 уравнения с 2-мя неизвестными: x и r
исключая x найдём r.
т.е
1ур. системы r^2 = 9^2 - x^2
2 ур системы r^2 = 5^2 - DH^2 , где DH-расстояние между точкой пересечения биссектрисы и стороны AC и точкой касания окружности к стороне AC.
DH надо будет выразить через x, для этого надо использовать самое известное свойство биссектрисы о том, что отношение отрезков на которые биссектриса угла делит сторону равно отношению прилежащих к углу сторон
тут много свойств, очень много, не надо зацикливаться на одном лишь св-ве касательных из одной точки.
попробуй записать систему какую-нибудь более рациональную