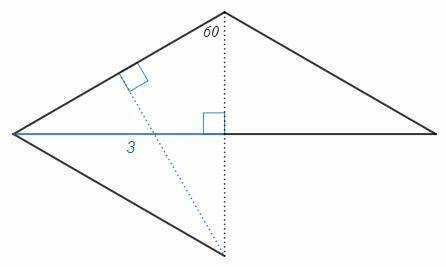
В равнобедренном треугольнике углы при основании равны, в треугольнике не может быть двух тупых углов, следовательно только угол против основания может равен 120.
Серединный перпендикуляр к основанию равнобедренного треугольника является также биссектрисой - делит угол против основания на два угла по 60, и медианой - делит основание на два отрезка по 3.
Точка пересечения серединных перпендикуляров является вершиной равнобедренного треугольника с основанием на боковой стороне (любая точка серединного перпендикуляра равноудалена от концов отрезка). Равнобедренный треугольник с углом 60 - равносторонний. В равностороннем треугольнике высоты равны.
Расстояние от точки пересечения серединных перпендикуляров до боковой стороны равно 3.
1)Два треугольника называются подобными, если их углы соответственно равны
1) да ; 2) нет
Вспомним 1-й признак подобия:
если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.
2)Любые два прямоугольных и равнобедренных треугольника подобны.
1) нет ;2) да
Верно. По первому признаку. Углы при основании равны 45°,а напротив основания 90°
3)Любые два прямоугольных треугольника подобны.
1) да 2) нет
В таких треугольниках мы можем утверждать только о равенстве одного угла-прямого. Ни для одного признака подобия этого недостаточно
Неверно
4 )Если две стороны одного треугольника соответственно пропорциональны двум сторонам другого треугольника, то такие треугольники подобны
1) да 2) нет
Более подходящие признаки
2-й -если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, образованные этими сторонами равны, то треугольники подобны. Равенство углов нам не дано. Утверждать не можем
3-й -: если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то треугольники подобны. Нам даны по 2 стороны. Утверждать не можем
5)Если два треугольника подобны, то их соответствующие стороны равны
1) да; 2) нет
3-й признак: если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то треугольники подобны.
6)Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
1) да ; 2) нет
Теорема верная.
7)Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники подобны.
1) да ; 2) нет
Это первый признак равенства. А,равные треугольники подобны
8)Если два угла одного треугольника соответственно пропорциональны двум углам другого треугольника, то такие треугольники подобны.
1) да ; 2) нет
Вспомним 1-й признак подобия:
если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.