Вершины вписанного квадрата лежат на описанной около него окружности. Диагональ квадрата - диаметр этой окружности.
Диагональ вписанного квадрата со стороной 8 см по теореме Пифагора DC=√(DH²+CH²) или DC=СН:sin45°=8√2, ⇒ радиус ОН =D:2=4√2 см. (См. рисунок). Соединим вершины А и В шестиугольника с центром О вписанной в него окружности.
Центральный угол АОВ=360°:6=60°, треугольник АОВ - равносторонний. Радиус вписанной окружности является его высотой. сторона АВ=АО=ОН:sin60°=(4√2):√3/2=(8√2):√3 или 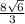 см
см
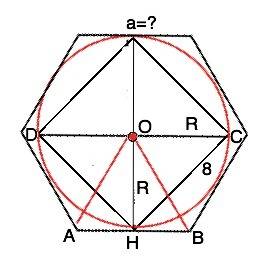
Итак, ответ - для АВ скрещивающаяся - СD, для DC - АВ. Впрочем, это одна и та же пара. В этой задаче есть еще одна пара скрещивающихся прямых. ВС скрещивается с АD.