Решение
Пусть M – точка пересечения медиан прямоугольного треугольника ABC с катетами AC и BC, P и Q – проекции точки M на AC и BC соответственно,
MP = 3, MQ = 4, K – середина BC.
Поскольку медианы треугольника делятся точкой пересечения в отношении 2 : 1, считая от вершины треугольника, то AC = 3PC = 3MQ = 12, BC = 9. Значит, AB = 15, SABC = ½ AC·BC = 54.
Поскольку высота треугольника ABC, проведённая из вершины прямого угла, равна AC·BC/AB = 36/5, то искомое расстояние равно 12/5.
ответ
12/5.
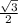 a ⇒
a ⇒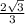 h
h 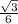 a =
a =  h
h 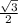 a ⇒
a ⇒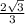 h =
h = 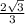 m =
m = 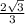 l
l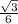 a =
a =  h =
h =  m =
m =  l
l h = 10 см
h = 10 см h = 1,4 (м)
h = 1,4 (м) h = 1
h = 1 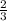 (см)
(см) h = 1,2 (см)
h = 1,2 (см) h = 3,7 (см)
h = 3,7 (см) m = 7 (см)
m = 7 (см)  m = 0,3 (мм)
m = 0,3 (мм)  m = 2
m = 2 (дм)
(дм)  m = 1,8 (см)
m = 1,8 (см)  m = 12,4 (см)
m = 12,4 (см)  l = 18 (мм)
l = 18 (мм)  l = 2
l = 2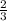 (м)
(м)  l = 24 (см)
l = 24 (см) l = 3,2 (см)
l = 3,2 (см)
Треугольник abc - равнобедренный с углами при основании ас равными 30 (углы bac=cab=bca так как ас биссектриса, а bc параллельна ad). Тогда по теореме косинусов в тр-ке abc ac² = ab²+ab² - 2*ab*Cos120° = 2*ab²*(1,5) = 3*ab².
В прямоугольном тр-ке acd по Пифагору ac² = 4cd² - cd² = 3cd².
Имеем: 3*ab² = 3cd², то есть ab = cd. Тогда периметр трапеции 35 = 5ab, откуда ab = 7см