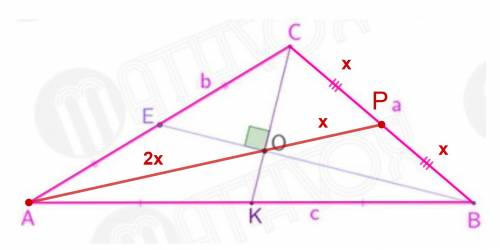
1) Проведем медиану AP, ⇒ CP = PB.
2) AO:OP = 2:1 (по свойству пересекаемых медиан)
3) ΔCOB — прямоугольный, т.к. CO⊥BO (CO∈CK, BO∈BE, CK⊥BE по условия задачи)
4) OP — медиана ΔCOB, т.к. ΔCOB — прямоугольный, CP = PB, а медиана делит сторону, на которую опущена, только в прямоугольном треугольнике, и эта сторона — гипотенуза, а угол, с которого проведена медиана — прямой.
Следовательно, OP = 1/2CB, или OP:CB = 1:2
5) AP:CB = (AO+OP):CB = (2+1):2 = 3:2.
ответ: отношение третьей медианы к соответствующий стороне — 3:2.
Находим координаты векторов и модули (вложение 1).
Находим модуль вектора а, скалярное произведение векторов а и b, угол между векторами c и d (вложение 2).
Приводим более подробное решение по определению угла меду векторами c и d (пусть они записаны как a и b).
Найдем скалярное произведение векторов:
a · b = ax · bx + ay · by + az · bz = 2 · 5 + (-9) · (-1) + (-10) · 5 = 10 + 9 - 50 = -31 .
Найдем длины векторов:
|a| = √ax2 + ay2 + az2 = √22 + (-9)2 + (-10)2 = √4 + 81 + 100 = √185 .
|b| = √bx2 + by2 + bz2 = √52 + (-1)2 + 52 = √25 + 1 + 25 = √51 .
Найдем угол между векторами:
cos α = (a · b ) / |a||b| .
cos α = -31 / (√185*√51) =
= - 31/√9435 = -31*√9435 / 9435 ≈ -0.319146.