Как расположены данные прямые?
Объяснение:
1. {4х+5у−1=0 ,а₁=4 ,в₁=5,
{12х +15у−8=0 ,а₂=12 ,в₂=15.
Проверим условие параллельности 4:12=5:15 , 1/3=1/3 верно, значит прямые параллельны.
2. {14х+2у−24=0 ,а₁=14 ,в₁=2 ,
{8х−56у+1=0 ,а₂=8 ,в₂=-56.
Проверим условие параллельности 14:8=2:(-56) , 7/4=-1/28 неверно, значит прямые не параллельны.
Проверим условие перпендикулярности 14*8=-(-56*2) ,112=112 верно, значит прямые перпендикулярны .
3.{12х+55у−19=0 , а₁=12 ,в₁=55 ,
{7х−12у+1=0 ,а₂=7 ,в₂=-12.
Вижу сразу , что не параллельны, т.к числа не пропорциональны и.Не перпендикулярны , т.к произведения разных знаков. Значит пересекаются .
================================================
PS. Если прямые заданы в виде а₁х+ в₁у+с₁=0, а₂х+ву₂+с₂=0 , то
- прямые параллельны если 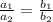 ;
;
-перпендикулярны если а₁*а₂ = в₁*в₂ .
Одна сторона прямоугольника равна х, х>0, вторая у, у>0. Площадь прямоугольника S = xy = 2 откуда y = 2/x. Рассмотрим функцию:
P(x)=2х+2у=2х+2*2/х=2х+4/х
Найдем производную этой функции, приравняем к нулю, получим критические точки
2-(4/х²)=0, откуда 4-2х²=0
х²≠0, х=±√2
Поскольку отрицательный корень x = -√2 не подходит по смыслу задачи, то берем критическую точку х=√2, разбиваем ею числовую ось и проверяем, какие знаки принимает производная на интервалах (0;√2);(√2;+∞)
(0)___-(√2)+
Производная функции при переходе через точку x = √2 меняет знак с минуса на плюс, поэтому х=√2 - точка минимума функции.
у=2/√2=√2
А наименьший периметр прямоугольника будет равен 4√2, если обе стороны равны √2, т.е. когда прямоугольник превратится в квадрат.
всего 2+4+6 = 12 частей
первая часть 2/12=1/6
вторая 4/12=1/3
третья 6/12=1/2