Объяснение:
2. Найдём площадь ромба с заданными размерами:
S=ha=21*14 см²
S(квадрата)=b²=21*14 ⇒ b=√(21*14)=√(2×3×49)=7√6 см.
ответ: д)
3. Площадь трапеции (любой) находится как произведение полусуммы оснований на высоту. Всё дано, подставляй и считай:
S=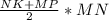
=(5+10)/2*4=7,5*4=30 см².
ответ: с)
ответ: 9 см и 23 см
Пусть трапеция АВСD, а ВК - биссектрисса тупого угла АВС. Поскольку она параллельна боковой стороне СD, то ВСDК - параллелограмм
Угол СDК равен углу АВК т.к. ВК - биссектриса.
Угол СDК равен углу КВС как противолежащие углы параллелограмма.
Угол СDК равен углу А, как углы при основании равнобокой трапеции. Следовательно, угол АВС равен двум углам А, и угол А + угол АВС =180° отсюда угол А = 60°, угол АВК = 60° и треугольник АВК - равносторонний АВ = АК = BK = 14, значит ВС + КD = 60 - (14*3) = 18. ВС = 18 : 2 = 9 см
АD = 9 + 14 = 23 см.
1) Sквадр=Sромба
а²=в*h; где а и в - стороны квадрата и ромба; h - высота
а²=21*14
а=√(21*14)=√(7*3*7*2)=7√6 см - Д)
2) Smnkp=(MP+NK)*MN/2=(5+10)*4/2=30 cм² - С)
(полусумма оснований на высоту).