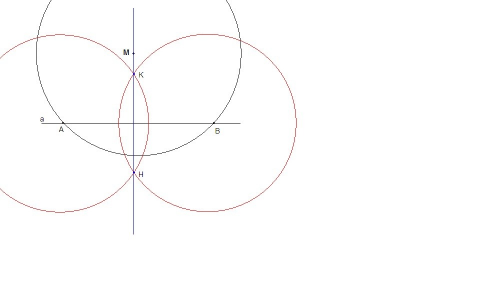
Дана прямая а и точка М, не лежащая на ней.
Проводим дугу с центром в точке М (черная), произвольного радиуса, большего расстояния от точки М до прямой.
Получили две точки пересечения дуги и прямой а. Обозначим их А и В.
Теперь построим две окружности (красных), с центрами в данных точках, произвольного одинакового радиуса (большего половины отрезка АВ).
Точки пересечения этих окружностей назовем К и Н.
Проводим прямую КН.
КН - искомый перпендикуляр к прямой а.
Доказательство:
Если точка равноудалена от концов отрезка, значит она лежит на серединном перпендикуляре к отрезку.
АК = КВ как равные радиусы, значит К лежит на серединном перпендикуляре к отрезку АВ.
АН = НВ как равные радиусы, значит Н лежит на серединном перпендикуляре к отрезку АВ.
КН - серединный перпендикуляр к отрезку АВ.
МА = МВ как равные радиусы черной окружности, значит и точка М лежит на прямой КН, т.е. перпендикуляр к прямой а проходит через точку М.
Дана прямая а и точка М, не лежащая на ней.
Проводим дугу с центром в точке М (черная), произвольного радиуса, большего расстояния от точки М до прямой.
Получили две точки пересечения дуги и прямой а. Обозначим их А и В.
Теперь построим две окружности (красных), с центрами в данных точках, произвольного одинакового радиуса (большего половины отрезка АВ).
Точки пересечения этих окружностей назовем К и Н.
Проводим прямую КН.
КН - искомый перпендикуляр к прямой а.
Доказательство:
Если точка равноудалена от концов отрезка, значит она лежит на серединном перпендикуляре к отрезку.
АК = КВ как равные радиусы, значит К лежит на серединном перпендикуляре к отрезку АВ.
АН = НВ как равные радиусы, значит Н лежит на серединном перпендикуляре к отрезку АВ.
КН - серединный перпендикуляр к отрезку АВ.
МА = МВ как равные радиусы черной окружности, значит и точка М лежит на прямой КН, т.е. перпендикуляр к прямой а проходит через точку М.