ответ: Такого треугольника не может быть.
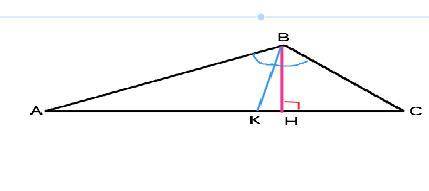
Объяснение: Биссектриса делит угол 130° на 2 равных по 65°.
Высота отсекает от треугольника прямоугольный треугольник с острым углом между высотой и боковой стороной 15°. (65°-50°=15°). Сумма острых углов треугольника 90°. Поэтому второй острый угол этого треугольника будет 90°-15°=75°. Получится, что сумма двух углов треугольника 130°+75°=205°, чего быть не может. А есть ведь ещё и третий угол.
Встречается подобная задача, где угол между высотой и биссектрисой 10°. Тогда решение возможно. Углы при основании получим 35° и 15°. При проверке сумма углов треугольника 130°+35°+15°=180°.
Подробное решение такой задачи дано мной на
O ((0+8)/2 ; (4-2)/2) = (4;1)
R=√8^2+(4+2)^2 /2 = 10/2=5
(x-4)^2+(y-1)^2=25