x - кусок медианы к боковой стороне между точкой пересечения и стороной.
Основание 2*x*√2; боковая сторона 2*x*√5; sin(A/2) = 1/√10; cos(A/2) = 3/√10; sin(A) = 3/5; cos(A) = 4/5
Так телеграфно :))) Основание выражено через х из треугольника, образованного кусками медиан от вершин до точки пересечения. Половина боковой стороны является гипотенузой в другом прямоугольном треугольнике - там катеты х и 2*х;
Дальше очевидно.
Если нужно искать решение, а формула для синуса удвоенного угла пока не проходилась (бывает такое), то надо найти высоту (через х, конечно), потом площадь, потом отсюда - высоту к боковой стороне (просто поделив площадь на боковую сторону), и синус уже перед нами :))) а если еще и теорему Пифагора применить для вычисления отрезка боковой стороны от вершины до основания высоты к ней, то и косинус тут же найдется. Тут что приятно - там египетский треугольник (3,4,5) получится (высота, боковая сторона и часть другой боковой стороны).
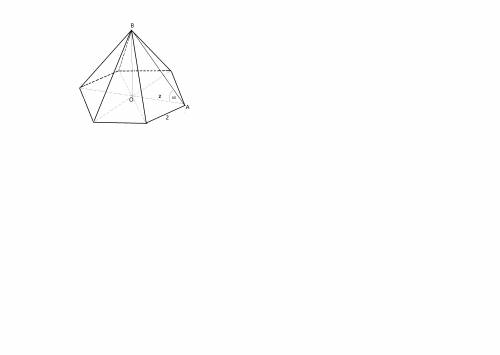
Объем пирамиды равен одной трети произведения ее высоты на площадь основания.
V=⅓ S∙h
Основание правильного шестиугольника состоит из шести правильных треугольников.
Площадь правильного треугольника находят по формуле:
S=(а²√3):4
S=4√3):4=√3
Площадь правильного шестиугольника в основании пирамиды:
S=6√3
Высоту найдем из прямоугольного треугольника АВО:
Так как ребро образует с с диагональю основания угол 60°, высота пирамиды ВО равна
H=ВО=2:ctg (60°)= 2·1/√3=2√3
Можно найти высоту и по т. Пифагора с тем же результатом.
V= 2√3∙6 √3:3=12 (кубических единиц)
сумма углов треугольника 180
или А+В+С=180
А=180-В-С=180-40-40=100
тогда смежный угол Д при вершине С равен А+В=100+40=140 градусов)