Окружность с центром О.
ВС - диаметр.
А ∈ окружности с центром О.
∠АОС = 35°
Найти:∠ВАО - ?
Решение:
Так как АО и ОВ - радиусы данной окружности с центром О ⇒ △ВОА - равнобедренный.
∠ОВА = ∠ВАО, по свойству равнобедренного треугольника.
Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним.
⇒ ∠ВАО + ∠ОВА = 35° (∠АОС = 35°, по условию)
Так как ∠ОВА = ∠ВАО, по свойству ⇒ ∠ОВА = ∠ВАО = 35°/2 = 17,5°
Так как АО и ОВ - радиусы данной окружности с центром О ⇒ △ВОА - равнобедренный.
∠ОВА = ∠ВАО, по свойству равнобедренного треугольника.
Сумма смежных углов равна 180°.
∠АОС смежный с ∠ВОА ⇒ ∠ВОА = 180° - 35° = 145°
Сумма углов треугольника равна 180°.
⇒ ∠ВАО = ∠ОВА = (180° - 145°)/2 = 17,5°
ответ: 17,5°.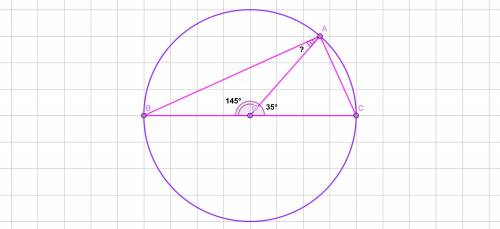
Объяснение:
1) Т.к. АВ=ВС, то треугольник АВС-р/б, следовательно, ВD - медиана, биссектриса, высота.
Т.к. ВD - биссектриса, то в треугольнике АВD угол АВD= 120°:2=60°
Т.к. ВD - высота, то в треугольнике АВD угол АDВ = 90°
Сумма углов треугольника равна 180°, следовательно, угол ВАD = 180°-(60°+90°)=180°-150°=30°.
2) Мы узнали, что угол ВАD=30°, найдём длину ВD.
Треугольник АВD - прямоугольный.
В прямоугольном треугольнике катет, лежащий напротив угла в 30° равен половине гипотенузы.
Угол ВАD = 30°, угол ВАD лежит напротив ВD, следовательно ВD = 0,5АВ=0,5×18=9 (см).
ответ: 1) 60°, 90°, 30°.
2) 9 см.
Вот чертёж, дано, надеюсь, напишешь.
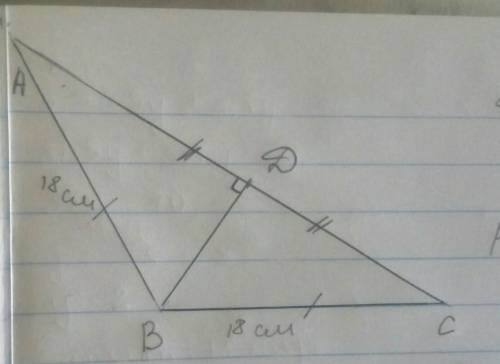
Медиана, проведённая к большему катету, равна 5√13 ≈ 18,03; гипотенуза делится точкой касания с вписанной окружностью на отрезки длиной 15 и 10.
(см. рисунок - в прикреплении)
Объяснение:
1) Медиана АМ, проведённая к большему катету ВС, делит его на 2 равных отрезка СМ = МВ = 10, и, таким образом, является гипотенузой в прямоугольном треугольнике МСА с катетами МС = 10 и АС = 15. Согласно теореме Пифагора, гипотенуза АМ равна корню квадратному из суммы квадратов катетов:
АМ = √(МС² + АС²) = √(10² + 15²) = √(100 + 225) = √325 = √(25 · 13) = 5√13 ≈ 5 · 3,6056 ≈ 18,03
2) Радиус r окружности, вписанной в прямоугольный треугольник, рассчитывается по формуле:
r = (a + b - c) : 2,
где а и b - катеты прямоугольного треугольника, с - его гипотенуза.
Гипотенуза АВ прямоугольного Δ АВС равна:
АВ = √(АС² + ВС²) = √(15²+20²) = √(225 + 400) = √625 = 25
Таким образом, радиус окружности, вписанной в Δ АВС, равен:
r = (АС + ВС - АВ) : 2 = (15 + 20 - 25) : 2 = (35 - 25) : 2 = 10 : 2 = 5
3) Вписанная окружность касается катета АС в точке D, а гипотенузы АВ в точке Е. Так как CD = r = 5, то АD = АС - СD = 15 - 5 = 10.
Отрезки касательных, проведённых к окружности из одной точки, равны.
Следовательно, AD = AE = 10
4) ВЕ = АВ - АЕ = 25 - 10 = 15
Таким образом, гипотенуза АВ делится точкой касания Е с вписанной окружностью на отрезки ВЕ длиной 15 и АЕ длиной 10.
ответ: медиана, проведённая к большему катету, равна 5√13 ≈ 18,03; гипотенуза делится точкой касания с вписанной окружностью на отрезки длиной 15 и 10.