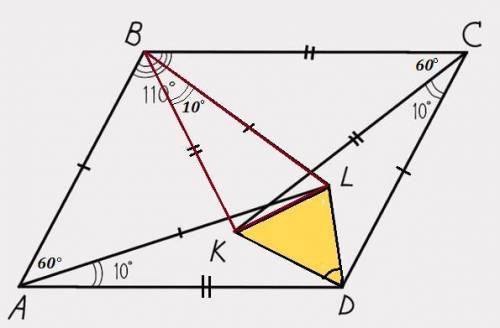
АВСД - параллелограмм, АД=ВС , АВ=СД , АД║ВС , АВ║СД .
∠АВС=110° ⇒ ∠ВАД=180°-110°=70° , ∠BCD=∠BAD=70° .
∠LAD=10° , тогда ∠BAL=70°-∠ДАL=70°-10°=60° .
∠KCD=10° , тогда ∠ВСК=∠ВСD-∠KCD=70°-10°=60° .
Рассмотрим два треугольника: ΔABL и ΔBCK .
Так как в ΔABL две стороны равны АВ=АL по условию , то ΔABL -равнобедренный. А так как ещё и угол в равнобедренном треугольнике ∠ВАL=60°, то этот треугольник - равносторонний, следовательно ВL=AB=AL=CD, ∠АВL=60° ⇒
∠CBL=110°-∠ABL=110°-60°=50° .
Аналогично, ΔВСК - равносторонний (КС=ВС по условию и ∠ВСК=60°) , следовательно ВК=ВС=СК=AD, ∠KBC=60° ⇒
∠KBL=∠KBC-∠CBL=60°-50°=10° .
Теперь рассмотрим три равных треугольника: ΔADL=ΔKCD=ΔKBL . Они равны по 1 признаку равенства треугольников:
AD=KC=BK , AL=CD=BL , ∠LAD=∠KCD=∠KBL=10° .
Отсюда следует, что стороны LD=KD=KL ⇒ ΔKLD - равносторонний, а в равностороннем треугольнике все углы равны 60°.
Значит, искомый угол ∠KDL=60° .
а) ∠ 1 = ∠ 4 = ∠ 5 = ∠ 8 = 20°,
∠ 2 = ∠ 3 = ∠ 6 = ∠ 7 = 160°.
b) ∠ 1 = ∠ 2 = ∠ 3 = ∠ 4 = ∠ 5 = ∠ 6 = ∠ 7 = ∠ 8 = 90°.
с) ∠ 1 = ∠ 4 = ∠ 5 = ∠ 8 = 32°,
∠ 2 = ∠ 3 = ∠ 6 = ∠ 7 = 148°.
Объяснение:
Задание а.
∠ 1 = 20°,
тогда ∠ 2 = 180° - ∠ 1 = 180° - 20° = 160°;
∠ 1 = ∠ 4 = 20° - как углы вертикальные;
∠ 1 = ∠ 5 = 20° - как углы соответственные при параллельных прямых а и b и секущей с;
∠ 5 = ∠ 8 = 20° - как углы вертикальные;
таким образом образом,
∠ 1 = ∠ 4 = ∠ 5 = ∠ 8 = 20°;
аналогично и остальные 4 угла равны между собой:
∠ 2 = ∠ 3 = ∠ 6 = ∠ 7 = 160°.
Задание b.
∠ 1 = ∠ 2 = 180° : 2 = 90°
Согласно доказательству в Задании а):
∠ 1 = ∠ 2 = ∠ 3 = ∠ 4 = ∠ 5 = ∠ 6 = ∠ 7 = ∠ 8 = 90°.
Задание с.
∠ 1 = 32°,
тогда ∠ 2 = 180° - ∠ 1 = 180° - 32° = 148°;
∠ 1 = ∠ 4 = 32° - как углы вертикальные;
∠ 1 = ∠ 5 = 32° - как углы соответственные при параллельных прямых а и b и секущей с;
∠ 5 = ∠ 8 = 32° - как углы вертикальные;
таким образом образом,
∠ 1 = ∠ 4 = ∠ 5 = ∠ 8 = 32°;
аналогично и остальные 4 угла равны между собой:
∠ 2 = ∠ 3 = ∠ 6 = ∠ 7 = 148°.
AC²=8²+15²=64+225=289 AC=17 см cos<C=15/17=0,882 sin<C=8/17=0,470