Найдём величину каждой из сторон параллелограмма.
Т.к. одна из сторон равна 5 см, противоположная ей также равна 5 см. Вместе они составляют 10 см.
Две остальные стороны в сумме дают 28 - 10 = 18 см. Отдельно каждая = 18:2 = 9 см.
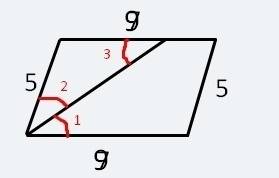
Угол 1 и угол 3 равны, т.к. они накрест лежащие.
Угол 1 и угол 2 равны, т.к. их образует биссектриса.
Благодаря тому, что угол 2 и угол 3 равны, образуется равнобедренный треугольник, в котором нам уже известна одна из сторон, которая равна 5 см. Т.к. треугольник равнобедренный, другая сторона, которая не биссектриса, также равна 5 см. Она же является частью ответа.
Чтобы найти второй отрезок, который образовала биссектриса, надо из длины основания вычесть длину уже известного отрезка: 9-5=4см.
ответ: биссектриса делит основание на отрезки 5 см. и 4 см.
1) Из условия следует, что острыми являются углы B и D. Рассмотрим прямоугольные треугольники ABC и ADC. Используя условие, что сумма острых углов прямоугольного треугольника равна 90∘, получим: ∠BAC=49∘, а ∠DCA=56∘. Следовательно, ∠BAD=90+49=139∘, а ∠BCD=90+56=146∘ и он наибольший в четырехугольнике.
2)Так как AB=BC и AD=CD, то треугольники ABC и ADC являются равнобедренными, а углы при основании в равнобедренном треугольнике равны. ∠A=∠BAC+∠CAD. ∠BAC=12(180∘−∠B)=12(180∘−60∘)=60∘, ∠CAD=12(180∘−∠D)=12(180∘−110∘)=35∘. ∠A=∠BAC+∠CAD=60∘+35∘=95∘.
120+68√14 м²
Объяснение:
∆АА1С- прямоугольный треугольник
По теореме Пифагора
АС=√(А1С²-АА1²)=√(15²-5²)=√(225-25)=
=√200 м
∆АСD- прямоугольный треугольник
По теореме Пифагора
DC=√(AC²-AD²)=√((√200)²-12²)=√56=
=2√14 м
Росн=2(АD+DC)=2(12+2√14)=24+4√14 м.
Sбок=Росн*АА1=5(24+4√14)=120+20√14 м²
Sосн=АD*DC=12*2√14=24√14 м²
Sпол=Sбок+2*Sосн=120+20√14+2*24√14=
=120+68√14 м²