
В С
А Д
дано:
уголА=40градусов
уголАВД=90градусов
ВС=СД
найти углы трапеции
рассмотрим треугольникАВД:
уголВДА=90-40=50градусов
уголВДА=углуСВД=50градусов (как накрест лежащие при ВС II АД и секущей ВД)
ТреугольникВСД равнобедренный, т.к. ВС=СД, следовательно углы при основании равны: уголДВС=углуВДС=50градусов
из этого треугольника находим уголС=180-50-50=80градусов
уголАВС=90+50=140градусов
уголСДА=50+50=100градусов (только это уже и не трапеция какая-то получается... т.к. угол при большем основании тупой. Может, в условии что не так?)
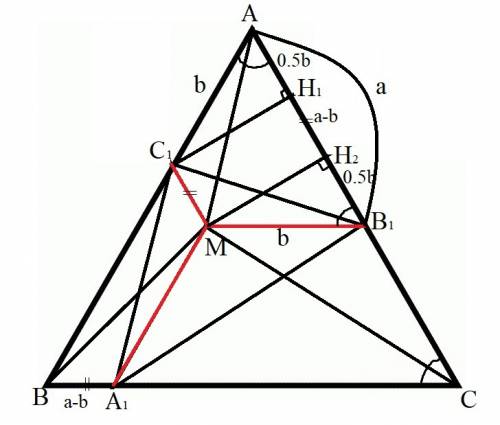
Пусть MA₁║AB, MB₁║BC, MC₁║AC.
Рассмотрим фигуру AB₁MC₁. Т. к. MC₁║AC ⇒ MC₁║AB₁, AC₁∦MB₁ ⇒ AB₁MC₁ - трапеция. Т. к. ∠A = ∠C, ∠C = ∠AB₁M как соответственные ⇒ ∠A = ∠AB₁M ⇒ AC₁ = MB₁, т. е. трапеция равнобедренная ⇒ B₁C₁ = AM как диагонали равнобедренной трапеции.
Аналогично рассуждая, C₁A₁ = BM, A₁B₁ = CM, что и требовалось доказать.
Пусть C₁H₁⊥AB₁, MH₂⊥AB₁. Тогда MC₁H₁H₂ - прямоугольник ⇒ H₁H₂ = C₁M. Т. к. A₁BC₁M - равнобедренная трапеция, A₁B = C₁M ⇒ A₁B = H₁H₂.
В прямоугольном треугольнике AH₁C₁ AH₁ = AC₁ * cos A = b * cos 60° = 0.5b. Аналогично B₁H₂ = 0.5b. Тогда H₁H₂ = AB₁ - AH₁ - H₂B₁ = a - 0.5b - 0.5b = a - b ⇒ A₁B = a - b.
ответ: a - b
DM≈7см
Решение:
S(∆ABC)=½*AC*AB*sinCAB
sin30°=1/2
S(∆ABC)=½*3*5*½=3,75см²
Теорема косинусов
СВ=√(АС²+АВ²-2*АС*АВ*cosCAB)
cos30°=√3/2
CB=√(5²+3²-2*5*3*√3/2)=
=√(25+9-15√3)=√(25+9-26)≈√8≈3.
S(∆ABC)=½*AM*CB;
AM=2*S(∆ABC)/CB=2*3,75/3=7,5/3=
=2,5см
∆DAM- прямоугольный треугольник
По теореме Пифагора
DM=√(DA²+AM²)=√(7²+2,5²)=
=√(49+6,25)=√55,25≈7см