Вариант решения.
Пусть в пирамиде ОАВС сторона АО=3, СО=4, ВО=12.
Для начала найдем длины сторон ∆ АВС.
По т. Пифагора АВ²=AO²+BO²=9+144=153
По т.Пифагора ВС²=ОС²+ОВ²=16+144=160
АС=√(АО²+ОС²)=√(9+16)=5
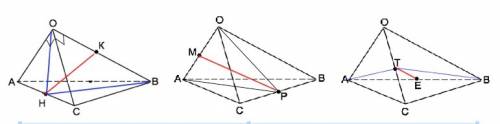
Обозначим середину АС - Н; ОВ =К; АО - М,; ВС - Р; ОС - Т; АВ -Е.
Расстояние между серединами АС и ОВ - медиана НК в ∆ ОНВ.
ОН- медиана прямоугольного АОС и равна АС:2=2,5
Формула медианы треугольника
М=0,5•√(2a²+2b²-c²), где а. b и с - стороны, причем с - сторона, к которой проведена медиана.
Тогдв М²=0,25•((2a²+2b²-c²) ⇒
ВН²=0,25•(2•AB²+2•BC²-AC²)=0,25•(2•160+2•153-25)=0,25•601
НК=0,5•√(2•OH*+2*BH*-OB*)=0,5√(12,5+0,5•601-144)=0,5•13=6,5
Аналогично вычисляются сначала медианы АР и ОР из ∆ АВС и ∆ СОВ, затем МР=6,5 из ∆ АРО и медианы АТ и ВТ из ∆ АОС и ∆АОВ, затем ТЕ=6,5 из ∆ АТВ.
Сумма найденных расстояний 3•6,5=19,5
a) Расстояние измеряется длиной перпендикуляра.
ODA =180-ADC =60
OE =OD*sin(ODA) =3√3/2
б) F, G - точки касания.
Центр O1 искомой окружности лежит на биссектрисе угла ADC.
O1DC =ADC/2 =60
DF =O1F/tg(O1DC) =r/√3
OF =OD+DF =3 +r/√3
Точка касания G лежит на линии центров.
OO1 =OG-O1G =2√3 -r
Теорема Пифагора, △OO1F
OO1^2 =O1F^2 +OF^2
(2√3 -r)^2 =r^2 +(3 +r/√3)^2
r^2 +18√3*r -9 =0
r =6√7 -9√3