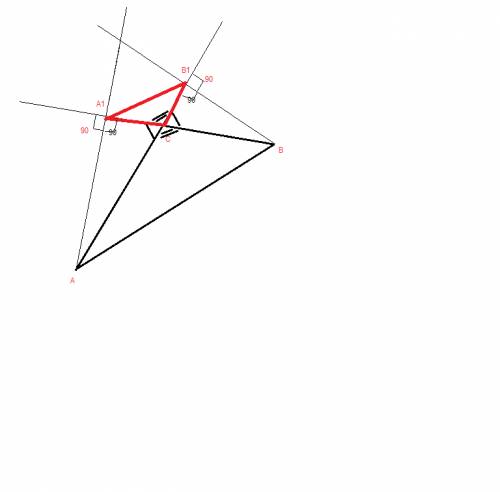
Доказать подобие треугольников А1СВ1 и АВС.
сделаем построение по условию
треугольники ACA1 и ВСВ1 - подобные по ПЕРВОМУ признаку подобия (по двум углам)
<AA1C=<BB1C=90 град
<ACA1=<BCB1 -вертикальные
следовательно , соответственные стороны относятся
СA1 / CB1 =CA / CB = k1 -коэффициент подобия для треугольников ACA1 и ВСВ1
отношение можно записать по-другому
СA1 / CA = CB1 / CB = k2 -коэффициент подобия для треугольников А1СВ1 и АВС.
т.е. треугольники А1СВ1 и АВС подобны по ВТОРОМУ признаку подобия
(если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы между этими сторонами равны)
пропорциональные стороны СA1 / CA = CB1 / CB
<A1CB1 = <ACB --вертикальные
доказано подобие треугольников А1СВ1 и АВС.
Доказать подобие треугольников А1СВ1 и АВС.
сделаем построение по условию
треугольники ACA1 и ВСВ1 - подобные по ПЕРВОМУ признаку подобия (по двум углам)
<AA1C=<BB1C=90 град
<ACA1=<BCB1 -вертикальные
следовательно , соответственные стороны относятся
СA1 / CB1 =CA / CB = k1 -коэффициент подобия для треугольников ACA1 и ВСВ1
отношение можно записать по-другому
СA1 / CA = CB1 / CB = k2 -коэффициент подобия для треугольников А1СВ1 и АВС.
т.е. треугольники А1СВ1 и АВС подобны по ВТОРОМУ признаку подобия
(если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы между этими сторонами равны)
пропорциональные стороны СA1 / CA = CB1 / CB
<A1CB1 = <ACB --вертикальные
доказано подобие треугольников А1СВ1 и АВС.
1) Пусть в одной части х см.
По условию катеты прямоугольного треугольника равны а = 3х см, b = 4х см, тогда по теореме Пифагора гипотенуза этого треугольника равна
с = √(а² + b²) = √(9x² + 16x²) = 5x (см).
2) В прямоугольном треугольнике
r = p - c
p = (3x + 4x + 5x) : 2 = 6x (см).
r = 6x - 5x = x (см).
3) По условию r = 4 см, х = 4 см.
S = 1/2•a•b = 1/2 • 3x • 4x = 6x² = 6•4² = 96 (см²).
4) Радиус окружности, описанной около прямоугольного треугольника, равен половине гипотенузы,
R = 1/2•c = 1/2 • 5 • 4 = 10 (см).
S = πR² = π•10² = 100π (см²).