Если провести сечение пирамиды через ее высоту перпендикулярно боковой грани, то получится прямоугольный треугольник CNK, где CN - высота пирамиды - один из катетов треугольника, NK - второй катет (след сечения основания пирамиды, N - прямой угол, K - угол равный 60 градусам (из условия), CK - гипотенуза (высота боковой грани пирамиды).
Центр O вписанного в пирамиду шара лежит на CN так, что ON равно его радиусу. Из точки O проведем перпендикуляр на гипотенузу до точки M. OM также должен быть равен радиусу шара. Рассматривая это построение, нетрудно показать, что точка O делит высоту CN в отношении 1:2. Таким образом радиус вписанного шара равен 3 (9/3).
Объем шара (4/3)*π*3*3*3 = π*36 или примерно 3.14*36 = 113
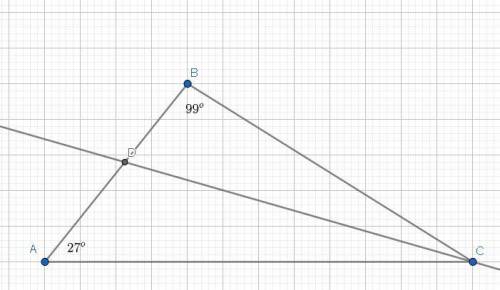
1. Для начала найдём все углы треугольника ΔABC.
<A = 27°; <B = 99° ⇒ <C = 180-(99+27) = 54°.
Так как биссектриса CD — делит угол <C на 2 равные части, то: <DCA = 54/2 = 27°.
Тоесть: <DAC == <DCA ⇒ DA == DC, что и означает, что треугольник ΔADC — равнобёдренный, так как боковые стороны равны.
2.
Угол — противоположный стороне DB — это <BCD, который в треугольнике ΔDBC — считается самым маленьким углом — 27°.
А сторона, противолежащая самому маленькому углу — считается самой маленькой стороной в определённом треугольнике.
В треугольнике ΔADC — опять же, самый маленький угол — <A (27°), а противолежащая ему сторона — DC, которая самая маленькая в треугольнике ΔADC.
И так как углы совпадают, то стороны равны, тоесть BD == CD.
Объяснение:
диагонали параллелограмма в точке пересечения делятся пополам
1) Рассмотрим ΔOCD
по теореме косинусов
b²=(d₁/2)²+(d₂/2)²- 2d₁d₂cos60°=(16/2)²+(10/2)²- 2(16/2)(10/2)(1/2)=
=8²+5²-2*5*8/2=64+25-40=50
b=√50=√(2*25)=5√2
2) Рассмотрим ΔOАD
∠AOD=180°-∠COD=180°-60°=120°
a²=(d₁/2)²+(d₂/2)²- 2d₁d₂cos120°=(16/2)²+(10/2)²- 2(16/2)(10/2)(-1/2)=
=8²+5²+2*5*8/2=64+25+40=130
a=√130 (м) ;b=5√2 (м)
3) P=2a+2b=2*5√2+2*√130=10√2+2√130=
P=10√2+2√120 (м)
4) S=d₁d₂sin60°=10*16(√2)/2=80√2
S=80√2 (м²)