Рисунок - во вложении.
Т.к. E и F - внутренние точки отрезка АВ, и по условию АЕ=BF, то
для EB=AB-AE и для AF=AB-BF следует, что EB=AF.
Рассмотрим прямоугольные ΔADF и ΔВСЕ. У них: 1) АD=BC (противолежащие стороны прямоугольника); 2) AF=EB (по доказанному выше). Значит, ΔADF = ΔВСЕ по двум катетам.
Из равенства этих треугольников следует, что ∠DFA=∠СЕВ. Отсюда, ΔEGF - равнобедренный с основанием EF, тогда GF=GE. Доказан пункт Б).
Т.к. АВСD - прямоугольник, то АВ║CD. Тогда ∠EFG=∠GDC(как накрестлежащие при секущей FD) и ∠FEG=∠GCD (как накрестлежащие при секущей ЕС). Отсюда, ΔDGС - равнобедренный с основанием DC, тогда DG=GC. Доказан пункт A).

Объяснение:
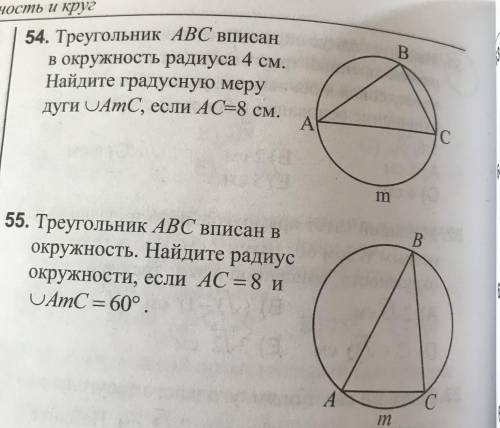
Радиус R=4 см.
Хорда АС=8 см. Следовательно хорда АС является диаметром окружности.
Угол, опирающийся на диаметр равен 90°. Вершина этого угла находится на окружности, значит этот угол вписанный и он равен половине градусной мере угла, на которую он опирается.
Исходя из этого, градусная мера дуги AmC равна 2*90°=180°.
или
диаметр отсекает половину окружности градусная мера которой 360°. Следовательно AmC=360°/2=180°.
***
Дуги АmC=60°. Значит вписанный угол АВС равен половине градусной мере дуги, на которую он опирается , т.е.30°. Тогда треугольник АВС - прямоугольный ∠АСВ=90°. Следовательно угол АСВ опирается на диаметр, половина которого равна АС=8 и диаметр равен D=2*АС=2*8=16.