1.Дано:
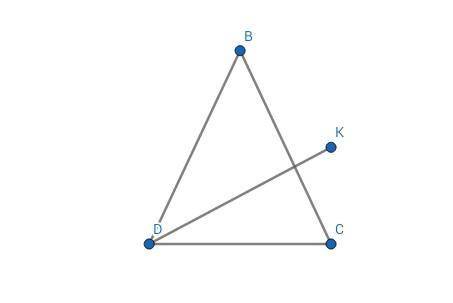
∆DBC.
DK - биссектриса.
∠CDK = 37°
∠DKC = 105°
Найти:
∠С; ∠D; ∠K.
Решение.
Сумма углов треугольника равна 180°
=> ∠С = 180 -(37 + 105) = 38°
Т.к. DK - биссектриса => ∠D = 37 × 2 = 74°
∠К = 180 -(74 + 38) = 68° (из 1 строчки решения)
ответ: 68°
2.Дано:
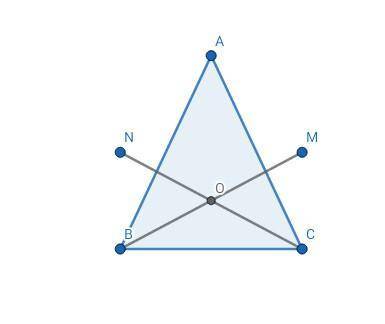
∆АВС - равнобедренный.
ВС - основание.
ВМ и CN - биссектрисы.
ВМ ∩ CN = O
∠A = 68°
Найти:
∠СВМ; ∠ВОС.
Решение.
Т.к. ∆АВС - равнобедренный => ∠В = ∠С
180 - 68 = 112 - сумма ∠В и ∠С.
∠В = ∠С = 112 ÷ 2 = 56°
Т.к. BM - биссектриса => ∠СВМ = 56 ÷ 2 = 28°
=> ∠NCB = ∠CBM = 28° (т.к. ∠В = ∠С)
Сумма углов треугольника равна 180°
∠ВОС = 180 -(28 + 28) = 124°
ответ: 28°; 124°.
Извините,у меня получилось только так на рисунке.Вообще точки должны лежать на сторонах и прямые не должны заходить за стороны треугольника.
Найдите площадь равнобедренной трапеции описанной, около окружности с радиусом 3, если боковая сторона трапеции делится точкой касания с окружностью в отношении 2:3
Объяснение:( опускаю объяснения как выбиралось отношение 2:3)
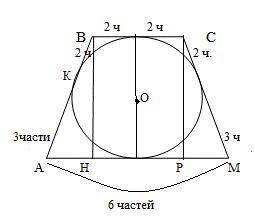
АВСМ-описанная трапеция около окр О(r=3) , АВ=СМ, К- точка касания , ВК:КА=2:3. Найти S.
S=1/2*Р*r , Р=2*АВ+ВС+АМ.
Пусть одна часть х, тогда АК=3х, КВ=2х , АВ=5х.
Т.к трапеция равнобедренная , то АВ=СМ=5х.
По свойству отрезков касательных АМ=3х+3х=6х и
ВС=2х+2х=4х.
Пусть ВН⊥АМ, СР⊥АМ⇒НВСР-прямоугольник и ВС=НР=4х . Значит РМ=АН=(6х-4х):2=1х.
ΔАВН прямоугольный , ВН=3+3=6 , по т.Пифагора АВ²=АН²+ВН²
25х²=х²+36, 24х²=36 , х=√(36/24)=6/(2√6)=√6/2.
Р=2*АВ+ВС+АМ=2*5х+4х+6х=20х , Р=20*(√6/2)=10√6.
S=1/2*10√6*3=15√6 ( ед²)
S=a*h1=15*3=45 см.кв.
S=b*h2=>h2=S/b=45/9=5 см.
Объяснение: