Question

1. Понятие числа. Виды чисел, действия над числами. 2. Комплексные числа. Мнимая единица. Действия над ними.
3. Приближенное значение величины и погрешности измерений.

4. Степень с рациональным и действительным показателями, свойства степеней.
5. Иррациональные уравнения их решения.
6. Корень п-ой степени, его свойства и правила сравнения корней.
7. Определение равносильности выражений с радикалами. Методы решения иррациональных уравнений.

8. Интегрирование, основные правила и формулы интегрирования.
9. Первообразная функции.
10. Неопределенный интеграл и его свойства. Табличные интегралы.
11. Определенный интеграл и его свойства. Формула Ньютона-Лейбница.

12. Синус, косинус, тангенс, котангенс угла. Обратные тригонометрические функции.
13. Радианное измерение дуг и улов. Тригонометрические функции числового аргумента.
14. Тригонометрические уравнения и их решений.
15. Четные и нечетные функции. Периодичность тригонометрической функции.
16. Формулы приведения.
17. Тригонометрическая функция y= tg(x). Ее свойства и график.
18. Тригонометрическая функция y= ctg(x). Ее свойства и график.
19. Тригонометрическая функция y= sin(x). Ее свойства и график.
20. Тригонометрическая функция y= cos(x). Ее свойства и график.
21. Радианное и градусное измерение дуг и углов. Единичная числовая окружность. Тригонометрические функции числового аргумента.
22. Основные тригонометрические тождества.
23. Формулы приведения.
24. Тригонометрические функции алгебраической суммы двух аргументов (формулы сложения).
25. Тригонометрические функции удвоенного аргумента.

26. Показательные и логарифмические функции, их графики и свойства.
27. Показательные и логарифмические уравнения их решения.
28. Показательные уравнения и неравенства
29. Логарифм числа. Основное логарифмическое тождество. Переход к новому основанию.
30. Свойства логарифмов. Десятичные и натуральные логарифмы
31. Логарифмические уравнения и неравенства.
32. Логарифм и его свойства.

33. Алгоритм исследования функций с производной Производная функции, её геометрический и физический смысл.
34. Формулы дифференцирования. Дифференцирование сложных функций.
35. Физические приложения производной. Уравнение касательной к графику функции.
36. Вторая производная, её физический смысл. Исследование функции на экстремум с второй производной.
37. Исследование функции на экстремум с производной.
38. Алгоритм исследования функции на экстремум.

39. Поверхность и объем куба. Диагональ куба.
40. Параллельность прямой и плоскости.
41. Параллельность прямой и плоскости (определение, теорема, следствия из теоремы).
42. Тела вращения, их объемы. Формулы.
43. Тело и поверхность. Многогранники и их виды. Развертка.
44. Аксиомы стереометрии и следствия из них.
45. Сечения цилиндра. Формула объема цилиндра.
46. Взаимное расположение двух прямых в пространстве.
47. Угол между векторами. Скалярное произведение векторов.
48. Векторы в пространстве. Действия над векторами. Прямоугольная (декартова) система координат в пространстве.
49. Векторы в пространстве. Векторное и скалярное произведение векторов. Признаки компланарности и коллинеарности векторов.
50. Перпендикуляр и наклонная. Угол между прямой и плоскостью.
51. Теорема о трех перпендикулярах.
52. Тело и поверхность. Многогранники, их вид. Объем прямоугольного параллелепипеда, прямой призмы, пирамиды. Правильные многогранники.
53. Параллельность прямой и плоскости. Параллельность плоскостей.
54. Тело вращения. Цилиндр. Сечения цилиндра. Площадь поверхности цилиндра, его объем.
55. Пирамида. Площадь поверхности пирамиды, ее объем.
56. Призма, параллелепипед, прямоугольный параллелепипед, куб и их свойства. Площадь поверхности призмы и параллелепипеда, их объемы.
57. Тело и поверхность. Многогранники, их виды формулы вычисления объемов. Развертка.
58. Уравнение сферы. Площадь поверхности сферы, объем шара.
59. Угол между векторами. Скалярное произведение векторов.
60. Координаты вектора. Действия над векторами, заданными в координатах.

Answer 1

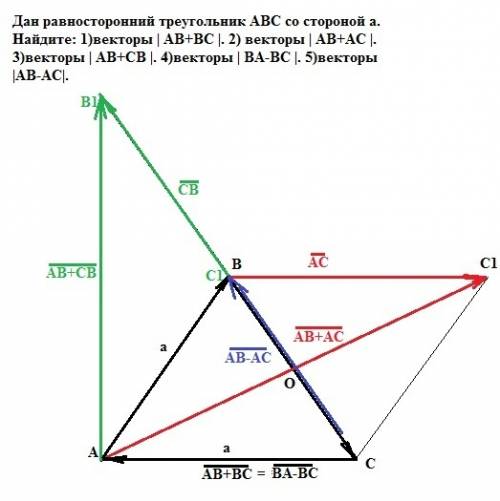
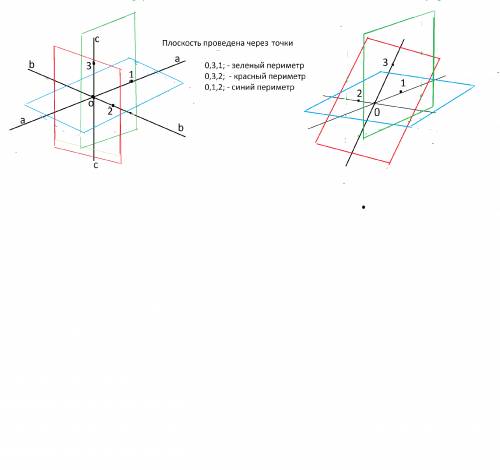
Объяснение:

gnbyggn