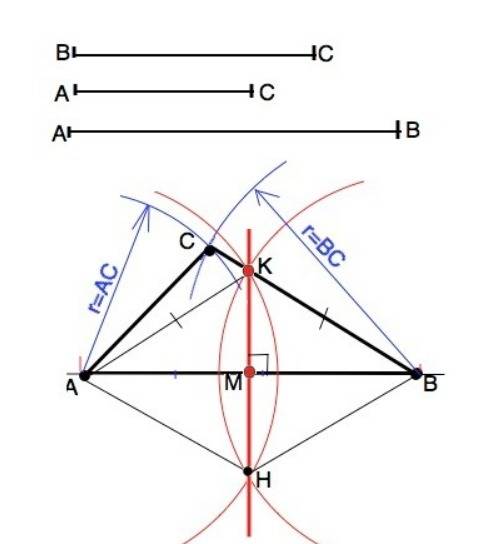
1). На произвольной прямой отложить отрезок, равный стороне АВ. Обозначить на концах отрезка вершины треугольника: точки А и В.
2) Из точки А как из центра раствором циркуля радиусом, равным длине стороны АС, начертить дугу.
3) Из т.В как из центра раствором циркуля радиусом, равным длине стороны ВС, начертить дугу до пересечения с первой дугой.
Точка пересечения дуг – вершина С искомого треугольника. Соединив А и С, В и С, получим треугольник со сторонами заданной длины.
б) Построение срединного перпендикулярна стандартное.
Из т.А и т.В как из центров провести полуокружности произвольного, но равного радиуса несколько больше половины АВ так, чтобы они пересеклись по обе стороны от АВ (т.К и т. Н).
Точки пересечения К и Н этих полуокружностей соединить.
Соединить А и Н, В и Н. Четырехугольник АКВН - ромб ( стороны равны взятому радиусу). Диагонали ромба пересекаются под прямым углом и точкой пересечения делятся пополам. =>
АМ=МВ и КМ перпендикулярно АВ.
КМ - срединный перпендикуляр к стороне АМ.
-----------
Точно так же делят отрезок пополам.
Объяснение:
пусть сторона основания a
Sполная =2Sоснования+Sбоковая=2Sоснования+4Sбоковой грани=
=2a²+4*8*a=246
2a²+4*8*a=246
2a²+32a-246=0
разделим на 2
a²+16a-123=0
отрицательный корень не рассматриваем
a=(-16+√(16²+4*123)/2=(-16+√(256+4*123)/2=
=(-16+√748)/2=(-16+√(4*187))/2=(-16+2√187)/2=-8+√187
=(√187)-8 (cм)
ответ сторона основания параллелепипеда (√187)-8 (cм)
Проверка
S=2a²+32a=2(-8+√187)²+32(-8+√187)=
=2(64-2*8(√187)+187)-32*8+32√187=
=128-(32√187)+374-256+32√187=128+374-256=246