Вычислите обьем правильной четырехугольной призмы, сторона и высота которой составляют соответственно - id2007888820200530 от milanakpoplove 30.05.2020 23:26

Question

Геометрия: Вычислите обьем правильной четырехугольной призмы, сторона и высота которой составляют соответственно 3√2 см и 5 см​

milanakpoplove · Accepted Answer

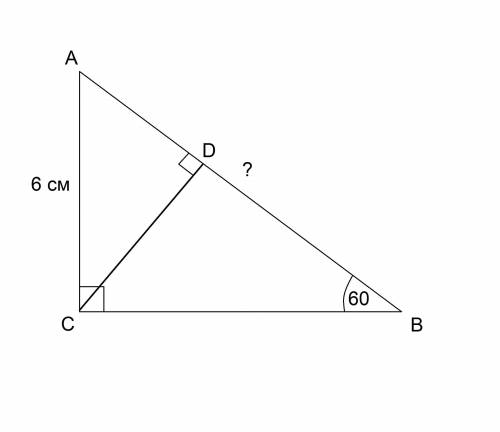
Дано: ΔABC - прямоугольный, ∠C = 90°, ∠ABC = 60°, AC = 6 см.

Найти: а) AB; б) CD

Решение: 1) Рассмотрим ΔABC: ∠ABC = 60°, ∠C = 90°, ∠A = 30° (т. к. 180° - (90° + 60°) = 30); Найдем сторону AB через синус угла ABC (синус острого угла равен отношению противолежащего катета к гипотенузе): sin60° = 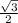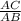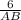$\frac{\sqrt{3}}{2}$ = $\frac{AC}{AB\\}$ = $\frac{6}{AB}$ ; Отсюда AB = 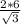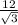$\frac{2*6}{\sqrt{3} }$ = $\frac{12}{\sqrt{3} }$ см.

2) Рассмотрим ΔACD, в котором ∠D = 90°, а ∠CAD = 30° (из 1); Согласно свойству прямоугольного треугольника с углом в 30°, катет, лежащий напротив угла в 30°, равен половине гипотенузы, следовательно, CD = 1/2*AC = 1/2*6 = 3 см.

ответ: а) 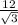$\frac{12}{\sqrt{3} }\\$ см; б) CD = 3 см.

решите задачу по геометрии! Очень вас. В прямоугольном треугольнике ABC угол С = 90 градусов, АС = 6

Вычислите обьем правильной четырехугольной призмы, сторона и высота которой составляют соответственно 3√2 см и 5 см​

MOGZ ответил

Вычислите обьем правильной четырехугольной призмы, сторона и высота которой составляют соответственно 3√2 см и 5 см