1) Так как на луче точки В и С можно расположить двумя то нужно рассмотреть оба. В первом случае, если порядок точек А В С, отрезок АВ будет равен 7,8-2,5=5,3 см. Во втором случае при порядке точек А С В отрезок АВ будет равен 7,8+2,5=10,3 см.
2) Углы, образованные пересечением двух прямых, являются смежными и вертикальными. Берем два смежных угла. По условию один угол меньше другого на 22°. Сумма смежных углов 180°. Находим меньший угол - (180°-22°):2=79° Больший угол равен 79°+22°=101°
1) 5,3 см и 10,3см
2) 79° и 101°
3) 18° и 162°
1)
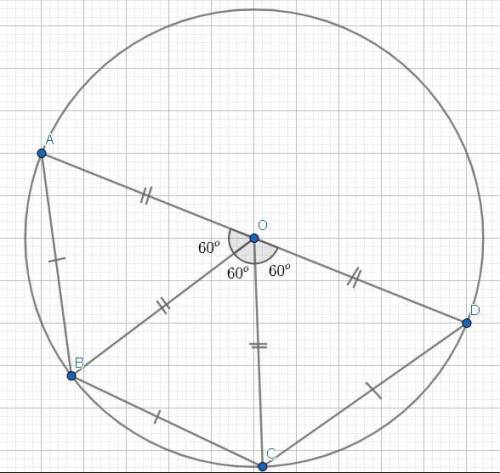
AB == BC == CD.
Проведём через вершины B & C — радиусы: BO == CO = r.
AO == OD = AD/2 = r (половина диаметра равна радиусу окружности).
Наши треугольники таковы: ΔAOB; ΔBOC; ΔCOD.
Учитывая информацию, данную нам задачей, и новые отрезки — найденные нами, мы составим определения: (AO == OD == OC == BO); (AB == BC == CD).
И так как каждый треугольник — имеет одну пару равных друг другу сторон (каждые 2 стороны в каждом треугольнике — радиусы), и равные основания (AB == BC ==CD), то по третъему признаку равенства треугольников: ΔAOB == ΔBOC == ΔCOD.
Что и означает, что: <AOB == <BOC == <COD ⇒ <COD == <BOC = 180/3 = 60°.
<BOD = <COD + <BOC = 60°+60° = 120°.
Вывод: <BOD = 120°.
2)
1.
Отрезки OA & OB — радиусы, так как каждый из них проведён с одной точки, находящийся на окружности, до её центра.
CO == OB = r.
<COB = 60° ⇒ <AOB = 180-60 = 120° (так как <AOB & <COB — смежные углы).
<AOB = 120°; OA == OB ⇒ <B == <AOB.
<AOB = (180° - <OAB)/2 = 30°.
AD — касательная, что и означает, что радиус, проведённый с точки касания до центра окружности — перпендикулярен этой касательной.
То есть: <OAD = 90°; <OAB = 30° ⇒ <DAB = 90-30 = 60°.
Вывод: <DAB = 60°.
2.
Проведём отрезки AO & OD.
AO == OD == CO == OB = r.
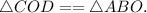
Эти треугольники равны по трём сторонам (третий признак равенства треугольников).
Тоесть: 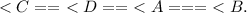
Как мы видим — накрест лежащие углы равны: <C == <B.
А первый признак параллельности прямых таков: если накрест лежащие углы друг другу равны, то: a║b.
Тоесть: AB║CD.
ответ: 60° .
Объяснение:
∠АВМ = 30° , бо sin∠ABM = k/2k = 1/2 ;
∠BDM = ∠MBD= ∠DBC ; ∠MBC = 90° - 30° = 60°;
∠ABD = 2*30° = 60° ;
ΔAOB - рівнобедрений , в якому один кут має 60° , тому він правильний . Отже, кут між діагоналями ∠АОВ = 60°.