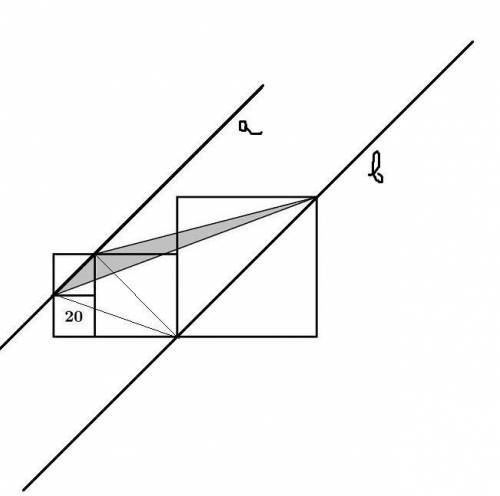
Рассмотрим множество треугольников, у которых две вершины расположены на диагонали маленького квадрата (на исходном рисунке в условии), а третья лежит на прямой, содержащей диагональ большого квадрата (см. мой рисунок). Заметим, что площади треугольников, входящих в это множество, попарно равны. Действительно, у всех треугольников общая сторона — диагональ малого квадрата, высоты, падающие на эту диагональ тоже равны, поскольку a ║ b.
Значит, площадь серого треугольника равна площади треугольника, указанного на моем рисунке. Площадь среднего квадрата равна 80. Теперь осталось следить за руками: (80+20+20)-40-10-60/2=70-30=40. Площадь равна 40.
AB = BC = CD = AD = a; P = 4a = S(бок) /H = 24; a = 6
треугольники ABD и BCD - равносторонние
S(сеч) = S(BDD1B1) = BD·H = 6·10 = 60 (см²)
2) Если все боковые ребра пирамиды наклонены к плоскости основания (прямоугольный треугольник ABC, ∠B = 90) под одинаковым углом (90 - 45 = 45), то около основания такой пирамиды можно описать окружность, а высота, опущенная из вершины на основание, падает в центр (точка O, лежит на середине гипотенузы) описанной около основания окружности.
AC = 2·4·tg(45) = 8
BC = AC·cos(30) = 4√3
AB = AC·sin(30) = 4
OH⊥AB; OH = BC/2 = 2√3
OK⊥BC; OK = AB/2 = 2
DH = √(OD² + OH²) = 2√7
DK = √(OD² + OK²) = 2√5
S(бок) = (1/2)(8·4 + (2√7)·4 + (2√5)·(4√3)) = 4(4 + √7 + √15) (см²) надеюсь