30°
Объяснение:
В данном случае нам очень знание всех формул на площадь. А именно через синус. Формула имеет вид
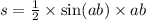
Где ab - угол между смежными сторонами и a и b длина этих сторон.
Зная синус угла между сторонами, мы найдем угол между сторонами по арксинусу.
Выразим синус
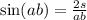
Подставим значения и получим 0.5
Если это была бы тригонометрия, то угол равнялся
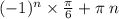
Где n - целое число.
Но в геометрии углы не могут быть отрицательными или больше 180°. Поэтому рассмотрим 2 варианта: 30° и 150°. Надо думать логически: напротив угла стоит сторона либо самая большая, либо самая маленькая (не факт, но наверняка). Рассмотрим случай с большей стороной.
Эта сторона будет больше 8; 9, например (на самом деле больше, но я просто привел пример). Как мы знаем, площадь треугольника равна полупроизведению основания и высоты. Тогда их произведение равно 12. Если наша сторона равна 8, то высота будет равна максимум 1.5. На самом деле, сторона это равна около 11. Попробуем проверить с формулы Герона. Не проходит, тогда правильный ответ 30°.
(Я вырезал часть решения с нахождением третьей стороны по теореме косинусов и подставлению в формулу Герона, но я посчитал, что сделал неправильно, поэтому оставил часть решения на вас, так как мое неоптимально)
1. Решение: пусть в равнобедренном треугольнике АВС АС - основание, АВ и ВС - боковые стороны, равные по 13 см, ВМ медиана, равная 5см.
Так как треугольник равнобедренный, ВМ - высота данного треугольника, АМ = МС и треугольники АВМ и СВМ равны.
АМ = 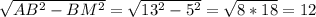 см
см
АС = 2*АМ = 24см
Р = 13 + 13 + 24 = 50см
S = 1/2 * ВМ * АС = 1/2 * 5 * 24 = 60см
2. во 2 задаче вы не написали чему равен угол D, пусть он будет α.
S = 1/2 * h (BC + AD)
h = CD * sinα
S = 1/2 * 10 * sinα (13 + 27) = 5*40 * sinα
Подставите значение угла D и получите ответ
3. Если в окружности пересекаются 2 хорды, то произведения их отрезков равны.
AM*MB = DM*MC = 120см
Составляем систему:
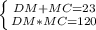
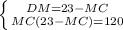
Работаем со вторым уравнением МС(23-МС) = 120
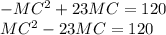
Решаем через дискриминант
D = 529 - 4*120 = 49
МС₁ = (23-7)/2 = 8
МС₂ = (23 + 7)/2 = 15
Подставляем в первое уравнение:
DM₁ = 23 - 8 = 15
DM₂ = 23-15 = 8
Значит, СМ и DM равны 8 и 15 см, или 15 и 8 см соответственно
4. Прямоугольный треугольник АВС (прямой угол С) вписан в окружность, значит центр окружности делит его гипотенузу на 2 одинаковые части. Гипотенуза данного треугольника АВ будет равна диаметру окружности, то есть 13 см.
катет ВС = 5см
АС = 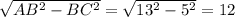 см
см
S = 1/2 * АС * ВС = 1/2 * 5 * 12 = 30см
1. АВ пересекает Окр(O;r) = D
2. ВС и ВА, СА и СВ, АС и АВ - касательные к окружности.
По свойству касательных (если из некотрой точки S проведены две касательные a и b к окружности, то отрезки касательных от точки S до точек касания А и В равны) BM=BD, КС=CM, AK=AD
2. Катет СВ=СМ+ВМ=4+8=12
3. Выразим отрезки касательных АК и АD через х.
Катет АС=КС+х, КС=4+х гипотенуза АВ=ВD+х, АВ=8+х
4. По теореме Пифагора:
АВ² = АС² + СВ²
(8+х)² = (4+х)² + 12²
64+16х + х² = 16 + 8х + х² + 144
16х + х² - 8х - х² = 16 + 144 - 64
8х = 96
х = 12
Следовательно, АК=12
ответ: АК=12
∠(ab)=30°
Объяснение:
∠(ab)=30°