Ледник — это скопление многолетнего льда на суше. В далёком несколько сотен тысяч лет назад, природные условия в Европе были такими, как в Антарктиде или Гренландии в наше время. Только ближе к экватору было немного теплее, чем теперь на побережье Северного Ледовитого океана. Снег, выпадавший на поверхность, не успевал таять, толщина его с каждым годом увеличивалась. Наконец под собственным весом он превратился в лёд. Ледники покрывали север Евразии, в том числе значительную часть территории Украины, юга России. Это была ледниковая эпоха. Ледники не раз наступали на материки. Ледниковые эпохи чередовались с межледниковыми. Мы живём в послеледниковую эпоху.
Важное значение для пополнения всех рек мира играют ледники. 16 млн кв. км - такая их общая площадь, это около 11% всей суши. Они содержат огромные запасы пресной воды. В России их огромное количество, площадью около 60 тыс. кв. км. Ледники России делят на два вида, по их образования:
Классификаций ледников, в том числе горных, существует очень много. Какие же разновидности их можно встретить в нашей стране? Снежные пятна. Скопление снега в пологих долинах и склонах. Ледники ступенеобразных склонов. Снежная масса собирается у теневого подножия горы и питается сошедшими лавинами. Висячие ледники. Располагаются на крутых склонах, как бы свешиваясь над ним. Они небольших размеров, но представляют опасность, так как могут сорваться вниз. Каровые ледники. Снежные массы в кресловидных долинах, с крутой задней стенкой. Ледники вулканических пиков. Занимают вершины гор. Переметные ледники. Они имеет общее начало - вершину хребта, но ставки в противоположные от него стороны. Норвежский тип. Такой вид ледников является переходным от горных к покровным. Ледяные шапки платообразных вершин растекается вниз. Дойдя до края, отдельными очагами спускаются вниз. Долинные располагаются в горных долинах.
Объяснение:
обозначим меньший треугольник АВС, больший треугольник А1В1С1,
по условию эти треугольники подобны...
Р(АВС) : Р(А1В1С1) = 4:5 (это и есть коэффициент подобия)
известно:
периметры подобных фигур относятся как коэффициент подобия,
площади относятся как квадрат коэффициента подобия
(объемы относятся как куб коэфф.подобия)
S(АВС) : S(А1В1С1) = 16:25
или 25*S(АВС) = 16*S(А1В1С1)
S(А1В1С1) = (25/16)* S(АВС) АВС--меньший треугольник
S(А1В1С1) - S(АВС) = 27 (см²) (по условию)
(25/16)*S(АВС) - S(АВС) = 27 (см²)
S(АВС)*((25/16) - 1) = 27 (см²)
S(АВС)*(9/16) = 27
S(АВС) = 27*16/9 = 3*16 = 48 (см²)
tg∠FAM = 0,001
Объяснение:
Дано: ∠ACB = 90°, CM = MB, AB = 101, BC = 20,∠CAF = ∠BAF
Найти: tg∠FAM - ?
Решение: Так как по условию угол ∠ACB = 90°, то треугольник ΔACB - прямоугольный, тогда по теореме Пифагора:
Так как по условию CM = MB и CM + MB = CB, то CM = MB = CB : 2 =
= 20 : 2 = 10. Рассмотрим прямоугольный (по условию ∠ACB = 90°) треугольник ΔACM. tg ∠CMA =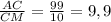 . CB = CF + FB ⇒ CF =
. CB = CF + FB ⇒ CF =
= CB - FB = 20 - FB. По теореме о биссектрисе для треугольника ΔACB (AF - биссектриса по условию): .
.
AC * FB = AB * (20 - FB)
99FB = 101(20 - FB)
99FB = 2020 - 101FB
200FB = 2020|:200
FB = 10,1
CF = 20 - FB = 20 - 10,1 = 9,9.
Рассмотрим прямоугольный треугольник ΔACF. tg∠CFA =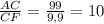 .
.
Угол ∠CFA смежный с углом ∠BFA, тогда по свойству смежных углов
∠CFA + ∠BFA = 180° ⇒ ∠BFA = 180° - ∠CFA. Рассмотрим треугольник ΔFAM. По теореме про сумму углов треугольника:
∠FAM + ∠AFM + ∠FMA = 180°;
∠FAM + 180° - ∠CFA + ∠FMA = 180°;
∠FAM = ∠CFA - ∠FMA
tg(∠FAM) = tg(∠CFA - ∠FMA) =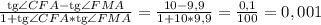 .
.