Известно, что диагональ в прямоугольном треугольнике является гипотенузой. Тогда мы можем найти периметр прямоугольного треугольника по формуле где a - любой катет, c - гипотенуза:
,
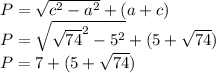Для того, чтобы вынести число из под корня, нужно записать подкоренное выражение как произведение множителей таким образом, чтобы из одного можно было извлечь арифметический корень.
Разложим на множители число 74:
74=1*2*37,
Не из одного множителя нельзя извлечь арифметический корень, чтобы получить целое число. Если разложить как 74=4*18,5, то выйдет:
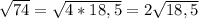, корень из 74 приблизительно равен 8,60 = 9
Таким образом,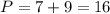 
ответ: P прямоугольного треугольника приблизительно равен 16 см.
P.S. Возможно в условии задачи допущена ошибка, так как по указанным вводным точное значение найти не предстоит возможным. Необходимо перепроверить с первоисточником. Прикрепите фотографию.
Точки M и N лежат в одной плоскости ABS, следовательно, через них можем провести прямую. След этой прямой — отрезок MN. Он видимый, значит, соединяем M и N сплошной линией.
Точки M и P лежат в одной плоскости ACS, поэтому через них проведем прямую. След — отрезок MP. Мы его не видим, поэтому отрезок MP проводим штрихом. Аналогично строим след PN.
Треугольник MNP — искомое сечение.
Если точка, через которую требуется провести сечение, лежит не на ребре, а на грани, то она не будет концом следа-отрезка.
Пример. Построить сечение пирамиды плоскостью, проходящей через точки B, M и N, где точки M и N принадлежат, соответственно, граням ABS и BCS.
построить сечение пирамиды плоскостью
Здесь точки B и M лежат в одной грани ABS, поэтому можем через них провести прямую.
Аналогично проводим прямую через точки B и P. Получили, соответственно, следы BK и BL.
Точки K и L лежат в одной грани ACS, поэтому через них можем провести прямую. Ее след — отрезок KL.
сечение пирамиды плоскостью
Треугольник BKL — искомое сечение.
Однако не всегда через
R=15/sin63°см
V=4500π/sin³63° см³
Объяснение:
∆ABC- прямоугольный треугольник
sin<BCA=AB/AC
AC=AB/sin<BCA=30/sin63°см диаметр цилиндра и диаметр шара.
R=AC/2=30/sin63°:2=30/sin63°*1/2=
=15/sin63° см
V=4πR³/3=4π(15/sin63°)³/3=4500/sin³63°