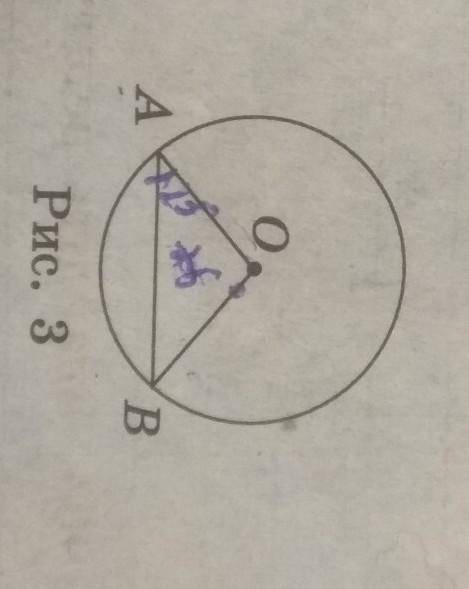
130°
Объяснение:
АО=АВ, так как радиусы окружности равны. Отсюда следует, что треугольник АОВ-равнобедренный. Угол ОАВ=углу ОВА=25°, так как у равнобедренного треугольника углы при основании равны. Сумма углов треугольника равна 180°.
Найдём угол АОВ:
Угол АОВ=180°-(25°+25°)=130°
ответ: (прописывать длины каждого из 12 ребер немного лень, напишу длины измерений)
ширина: 8
длина: 14
высота: 12
Объяснение:
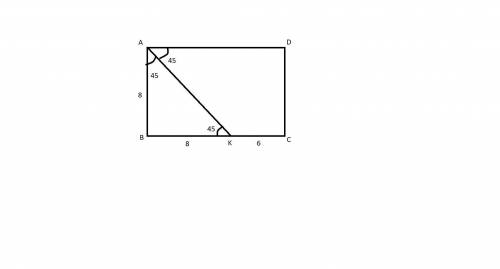
Поскольку AK - биссектриса прямого угла, то из принципа накрест лежащих углов при параллельных прямых имеем:
∠BAK = ∠KAD = ∠BKA = 45°
То есть ΔABK - равнобедренный.
Таким образом:
AB = BK = 8
BC = BK + KC = 8 + 6 = 14
У прямоугольного параллелепипеда 12 ребер, а именно по 4 ребра каждого из 3-x измерений.
Тогда сумма длин его измерений равна:
136/4 = 34 cм
Откуда найдем высоту параллелепипеда:
h = 34 - 8 - 14 = 12
Пусть дан треугольник ABC,где угол А = 45 °. ВН-высота ;
АН = 6 (см) , НС = 10 (см). Найдём S треугольника.
Рассмотрим треугольник АВН : угол А = 45 ° (по условию), значит угол АВН = 45 °. Следовательно треугольник равнобедренный и АН = НС = 6 (см) ,найдём АС.
АС = АН + НС = 6 + 10 = 16 (см)
Рассмотрим ВН: в равнобедренному треугольнике высота, проведенная к основанию, является медианой и биссектрисой.
Найдём высоту по формуле ВН=1/2*АС.
ВН = 1/2 * 16 = 8 (см)
S тр. = S= 1/2 АС * ВН
S тр. = 1/2 * 16 * 8 = 64 (см)
Объяснение:
1. ОА=ОВ=R(радіус)
2. Оскільки ОА=ОВ, то трикутник АОВ - рівнобедрений.
3. Оскільки трикутник АОВ - рівнобедрений, то кут ОАВ дорівнює куту ОВА.
4. Оскільки ку ОАВ=25°, то кут ОВА=25°.
5. Кут АОВ = 180°-(кут ОАВ+кут ОВА) = 180°-(25°+25°)=130°.