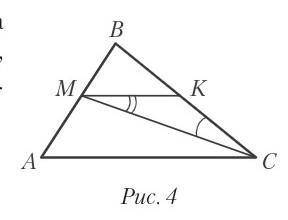
Дано: СМ - биссектриса треугольника АВС;
МК € АС;
угол ВСМ = 20°;
Найти: угол КМС -?
Т.к. СМ биссектриса треугольника АВС, то угол БСМ = углу МСА = 20°; и ВМ =МА
Следовательно, угол МСА = углу КМС = 20° (как на крест лежащие углы при МК || АС и секущей МС)
ответ: угол КМС = 20°
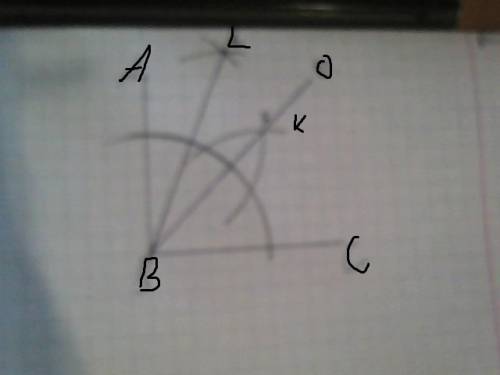
Сначало строишь прямой угол , далее проводишь биссектрису с циркуля :
1)построй прямой угол (думаю что сможешь это сделать )
2) выбрать произвольный раствор циркуля
3) иглу циркуля ставишь на сам угол
4) проведи дугу которая пересекает стороны угла
5) из точек касания дуги со сторонами угла не меняя раствор циркуля проведи дуги
6) пусть точка касания двух последних дуг будет называться K
7) соедини точку (в моем случае B с точкой K)
Теперь мы имее два угла по 45 градусов
С верхнего (ABO у меня) угла равного 45 градусам также проведи биссектрису в итоге 45/2=22°30' , наш нижний угол равен 45°
в итоге ( у меня угол LBC) равен 22°30'+45°=67°30'
ответ: 20°.
Объяснение:
Решение. Так как СМ - биссектриса, то ∠АСМ=∠ВСМ=20°.
∠АСМ=∠КМС, как внутренние накрест лежащие при МК║АС и секущей СМ. Следовательно, ∠КМС=20°.