Объяснение:
1)
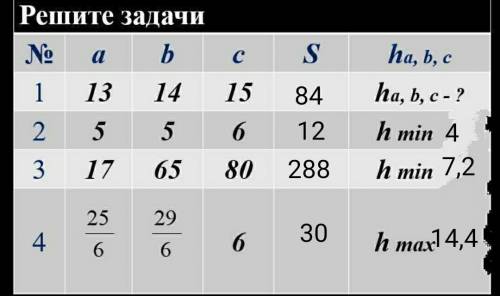
p=(a+b+c)/2=(13+14+15)/2=21см полупериметр
S=√(p(p-a)(p-b)(p-c))=√(21*8*7*6)=√7056=
=84см² площадь треугольника
h(a)=2S/a=2*84/13=168/13=12цел12/13 см
h(b)=2S/b=168/14=12 см
h(c)=2S/c=168/15=11,2 см.
ответ: площадь 84см²; высота проведенная к стороне а равна 12цел12/13см.; высота проведенная к стороне b равна 12см; высота проведенная к стороне с равна 12,2см.
2)
p=(a+b+c)/2=(5+5+6)/2=8см полупериметр
S=√(8(8-5)(8-5)(8-6))=√(8*3*3*2)=√144=
=12 см² площадь треугольника.
h(min)=2S/c=2*12/6=24/6=4см самая маленькая высота.
ответ: S=12см²; h(min)=4см.
3)
р=(а+b+c)/2=(17+65+80)=162/2=81см полупериметр треугольника.
S=√(81*64*16*1)=√82944=288см²
h(min)=2S/c=2*288/80=7,2см высота.
ответ: S=288см²; h(min)=7,2 см высота.
4)
р=(25/6+29/6+36/6)/2=90/6*1/2=45/6см полупериметр.
S=√(45/6*20/6*16/6*9/6)=√129600/√1296=360/12=30см². площадь треугольника
h(max)=2S/a=60:25/6=60/1*6/25=14,4 см максимальная высота
ответ: S=30см²; h(max)=14,4см.
Объяснение:
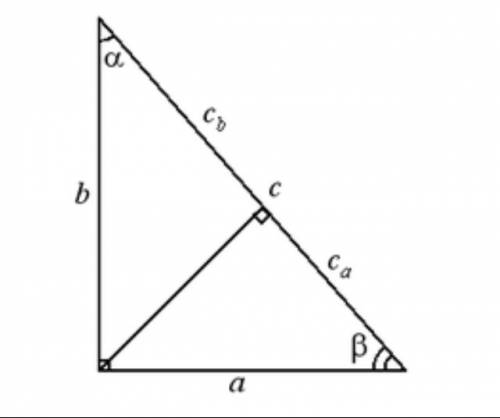
Дано: Окр.OR-описанная
ΔАВС - прямоугольный
ВК и СМ - медианы
Найти: cosα
1. Окр. OR - описана около ΔАВС ⇒СВ - диаметр (прямой угол опирается на диаметр)
2. Рассмотрим ΔАВС - прямоугольный.
Пусть меньший катет = a, больший - b.
Тогда:
Площадь треугольника:
По теореме Пифагора:
Составим систему:
По теореме Виета:
Или
Тогда АС=1; АВ=2.
3. Рассмотрим ΔАВК - прямоугольный.
По т. Пифагора
4. Рассмотрим Δ МАС - прямоугольный.
По т. Пифагора
5. Рассмотрим ΔКРС
Используем теорему косинусов:
Имеем