Вокруг треугольника с углами 30 градусов и 120 градусов описана окружность радиуса 3 см. Найдите площадь треугольника, составленного из медиан данного треугольника. ответ: √ см2.Решите !
треугольник с углами 30° и 120° -это равнобедренный треугольник))
две медианы равнобедренного треугольника (проведенные к боковым сторонам) равны... осталось найти медиану к основанию (m1) и медиану к боковой стороне (m2=m3)
составленный треугольник тоже получится равнобедренным...
его площадь можно найти по формуле Герона...
а можно найти (по теореме косинусов) косинус угла между медианами, найти (используя основное тригонометрическое тождество) синус этог угла и найти площадь по формуле S=0.5ab*sin(x)
1-cos(x) = 1/14
cos(x) = 13/14
sin(x) = √27 / 14
S = (1/2)*(63/4)*(√27 / 14) = 27√3 / 16 (ответ такой же))
Минут 5 ломал голову, с чего вообще начать) Потом вспомнил про подобие треугольников.
1. Проведём отрезки BD и AC (см. рисунок). Треугольники, образованные таким образом, будут подобными, поскольку у них равные углы при вершине K, а также угол C равен углу B (потому что они опираются на одну и ту же дугу), из чего по первому признаку подобия треугольников следует их подобие.
2. Значит, стороны треугольников пропорциональны. Очевидно, что если их сумма в два раза больше суммы другого треугольника, то и стороны тоже в два раза больше:
Минут 5 ломал голову, с чего вообще начать) Потом вспомнил про подобие треугольников.
1. Проведём отрезки BD и AC (см. рисунок). Треугольники, образованные таким образом, будут подобными, поскольку у них равные углы при вершине K, а также угол C равен углу B (потому что они опираются на одну и ту же дугу), из чего по первому признаку подобия треугольников следует их подобие.
2. Значит, стороны треугольников пропорциональны. Очевидно, что если их сумма в два раза больше суммы другого треугольника, то и стороны тоже в два раза больше:
ответ: S=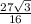
Объяснение:
треугольник с углами 30° и 120° -это равнобедренный треугольник))
две медианы равнобедренного треугольника (проведенные к боковым сторонам) равны... осталось найти медиану к основанию (m1) и медиану к боковой стороне (m2=m3)
составленный треугольник тоже получится равнобедренным...
его площадь можно найти по формуле Герона...
а можно найти (по теореме косинусов) косинус угла между медианами, найти (используя основное тригонометрическое тождество) синус этог угла и найти площадь по формуле S=0.5ab*sin(x)
1-cos(x) = 1/14
cos(x) = 13/14
sin(x) = √27 / 14
S = (1/2)*(63/4)*(√27 / 14) = 27√3 / 16 (ответ такой же))