
ответ: V=64√5см³
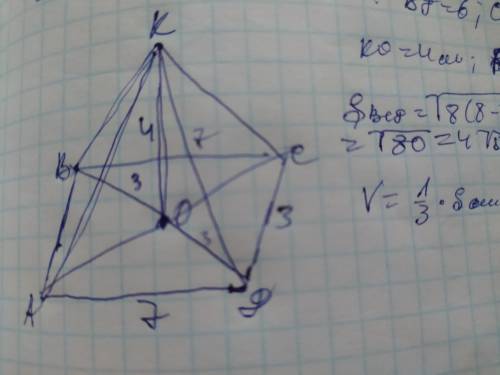
Объяснение: обозначим вершины пирамиды АВСД с высотой КО и диагоналями ВД и АС. Одна диагональ делит параллелограмм на 2 равных треугольника. Пусть ВД=6см. Рассмотрим полученный ∆ВСД. В нём известны 3 стороны и мы можем найти его площадь по формуле: S=√((p-a)(p-b)(p-c)), где а сторона треугольника а р-полупериметр:
Р=3+7+6=16см; р/2=16/2=8см
S=√8((8-7)(8-6)(8-3))=√(8×1×2×5)=
=√80=8√5см²
Так как таких треугольников 2, то площадь параллелограмма=8√5×2=16√5см²
Теперь найдём объем пирамиды зная площадь основания и высоту по формуле: V=⅓×Sосн×КО=
=⅓×16√5×4=64√5/3см³
Точка B(3,-2,2)
а) параллельна плоскости Oyz.
Уравнение плоскости, параллельной плоскости yOz, имеет вид: Ax + D = 0.
Подставляя в него координаты точки A, получим 3A + D = 0, или D = -3A.
Подставляя это значение в Ax + D = 0, получим
Ax - 3A = 0,
а сокращая на A, будем иметь окончательно
x - 3 = 0.
б) перпендикулярна оси Ox.
Так как плоскость перпендикулярна оси Ox, то она параллельна плоскости yOz, а потому ее уравнение имеет вид
Ax + D = 0.
Подставляя в это уравнение координаты точки A, получим, что D = -3A. Это значение D подставим вAx + D = 0 и, сокращая на A, будем иметь окончательно x - 3 = 0.
Подробнее - на -
ABCD-трапеция AO=OD, ∠ABD= 84° , ∠CBD=26°. Hайдите угол x.
Решение.
1)ΔAOD ~ΔCOB по 2-м углам :∠AOD=∠COB как вертикальные ,∠ADО=∠CОB , как накрест лежащие при АD║BC, ВD-секущая .Поэтому сходственные стороны пропорциональны :
АО:СО=DO:ВО, но АО=ВО ⇒СО=ВО.
Тогда диагонали равны :
АС=АО+СО
║ ║
ВD=DO+BO.
2)АО=DO ⇒ ΔАОD-равнобедренный⇒∠OAD=∠ODA.
3)∠B=26°+84°=110° . Тогда ∠BAD=180°-110°=70° , по т. о соответственных углах.
3) ΔADB=ΔADC по 2-м сторонам и углу между ними: AD-общая ,АС=ВD по п.1, ∠OAD=∠ODA по п. 2.
В ртсэр ⇒АВ=СD ⇒∠ВАD=∠ADC=70°.
4)Т.к. ∠АDB=∠CBD=20° как накрест лежащие , то х=70°-26°=44°.