Соединим центры окружностей с точками их пересечения, получим четырёхугольник, у которого все стороны равны (являясь радиусами).
Диагоналями этого четырёхугольника являются общая хорда и отрезок, соединяющий центры окружностей.
Известно, что четырёхугольник, у которого все стороны равны является ромбом(в частном случае - квадратом).
Диагонали получившегося ромба по свойству ромба перпендикулярны.
Следовательно общая хорда перпендикулярна отрезку, соединяющему центры окружностей, что и требовалось доказать.
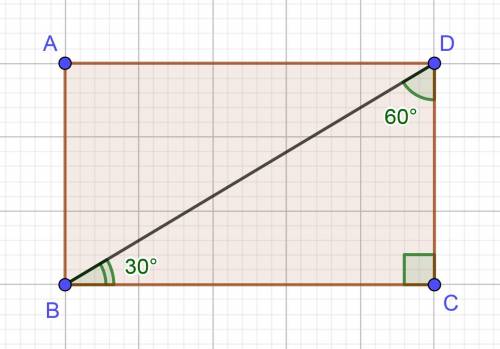
Нехай дано прямокутник ABCD, BD — діагональ, DC = 10 см, ∠BDC = 60°.
Р-мо BDC:
∠BCD = 90° — як кут прямокутника, отже ΔBDC — прямий, ∠BDC = 60° — за умовою, тоді ∠DBC за теоремою про суму кутів трикутника буде дорівнювати:
∠DBC = 180°−90°−60° = 30°.
По властивості катета, який лежить напроти кута 30°, гіпотенуза трикутника буде рівна:
BD = 2*DC = 2*10 = 20 (cm)
Знайдемо інший катет за т. Піфагора:
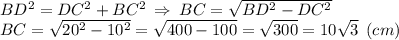
Підставимо значення у формулу площі прямокутника:

Відповідь: Площа прямокутника рівна 100√3 см² або приблизно 173,2 см².
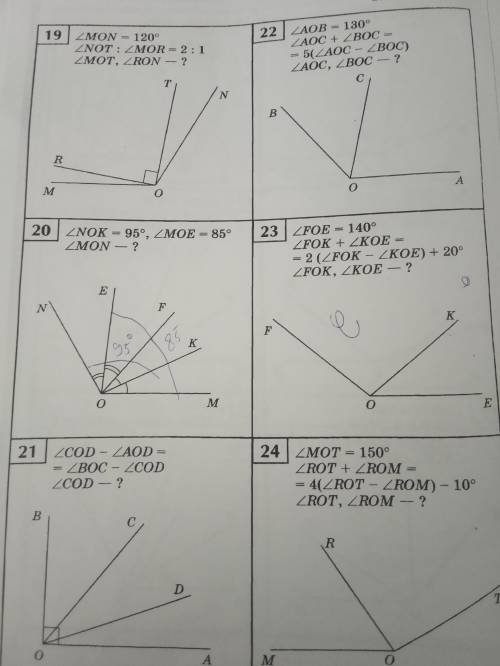
20) Угол с двумя дугами = х, с одной = у.
2х + у = 95
2у + х = 85. Сложим:
3х + 3у = 180, 3(х +у) = 180, х + у = 180/3 = 60.
ответ: искомый угол равен 2х + 2у = 2*60 = 120.
21)Пусть углы слева направо x, y, z.
По условию x + y + z = 90.
y - x = z - y, отсюда -x + 2y - z = 0.
Сложим 2 уравнения:
x + y + z = 90.
-x + 2y - z = 0. Сложим:
3у = 90.
ответ: у = 90/3 = 30.